Teachers constantly inspire me.  I love watching their development as they learn more about the curriculum they are teaching and as they develop their classroom practice.  Great teachers are always growing, reflecting, and adapting what they do to best meet pupil needs. 

This is never more evident than when teachers meet a new pupil who has needs that may be different from those that they have come across before.  For me, this is when we learn most as teachers and add most to our “teaching toolbox” but it is also when we can feel most vulnerable.  I am absolutely delighted therefore, that one inspirational teacher, Sam Hodges, has agreed to share her journey over the last academic year….  

When I was told that my new mixed-age Year 3/4 class would include a child who is registered blind, I had many questions going through my head wondering how I would have to change my teaching to ensure her needs were met. My biggest question was around maths.

As a school, we follow the HFL EDucation ESSENTIALmaths mixed-age planning and if you are a user of the planning, I am sure you will be aware of how visual the teaching is, especially in the younger years.

Where would I start? 

What would I need to do differently?

In this blog, I will share my teaching journey this year; what I have learnt, how I have developed my practice and how this has supported Olivia to make huge progress in her mathematical learning.  Olivia is not the child’s real name but is used for the purpose of maintaining anonymity.

Finding the right starting point

As Olivia was new to school and had limited prior maths teaching, it was essential to establish the right starting point. Based on my knowledge of the maths progression that we follow, I carried out my own assessments with Olivia and found that the best place to start would be building from foundations developed in the EYFS curriculum (Reception ESSENTIALmaths): focusing on building understanding of the number system and the value of numbers.

Using expert advice to build personalised provision

Advice from the HCC Visual Impairment Team identified that repetition is key to ensure learning is secured and that a child who has a visual impairment needs more repetition to secure their learning as they do not have visual aids to refer to around the classroom.

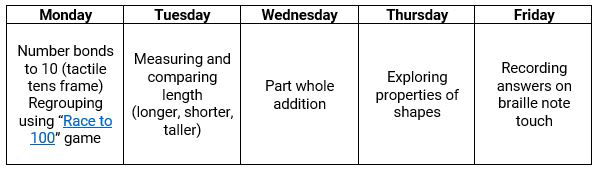
However, I knew that if I had to teach the same maths lesson every day each week, I would get bored of teaching it (let alone being a child doing the same thing each day) so we developed a rolling timetable for Olivia’s maths lesson. We created a carousel of activities that we would repeat each week.  An example is shown below.

 

 

Every half term, four of these activities changed. However, we felt it was necessary to keep the number and place value activities constant to secure key learning as her understanding continued to grow in this area.

Recognising and adapting to overcome challenges

There were several challenges in supporting Olivia’s understanding of the number system that we came across. 

Firstly, where most of us would use our fingers or objects to learn how to count, we would see the amount is increasing. However, for someone who is visually impaired, they do not have the same recognition. We tried many ways to support counting and found that concrete resources were the most beneficial. However, every time Olivia placed one down, she would not find it again on the table so rather than acknowledging she had counted to ten, she may still be at 1 or 2 as she could not feel the rest of the objects that were on the table.

To tackle this, we introduced small, lipped bowls, which reduced the area she was working in so every time she counted one, she placed one block into the bowl. This way she had a reduced space to scan, and she could feel the correct amount as well as scan to make sure she had not missed any.

 

 

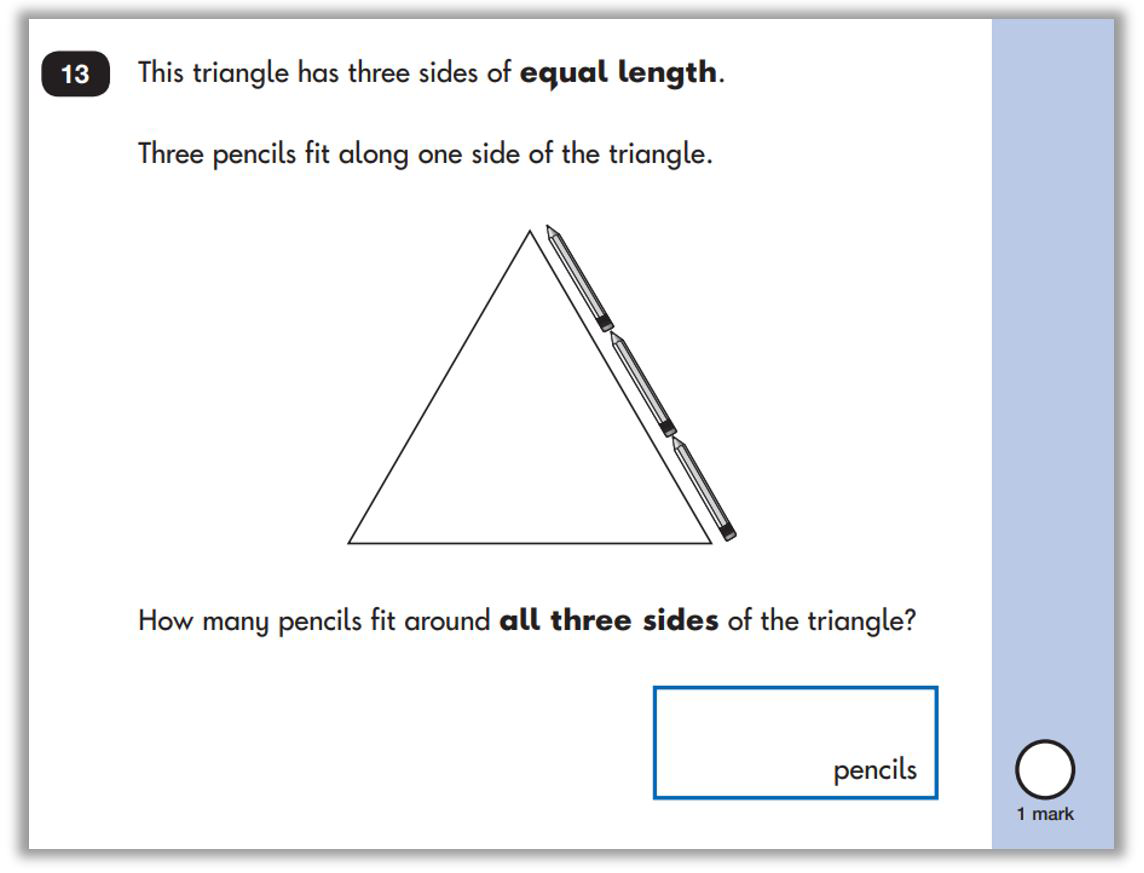
The next challenge we faced was addition.

The ESSENTIALmaths planning has a strong focus on the part whole model and regrouping when you get to a multiple of ten. We carefully built learning following the progression: firstly, building security in adding numbers within 10 which could be done using the lipped bowls and cubes. We continued using the lipped bowls and cubes for this, as they were by now familiar resources, and we introduced the concept of two parts making the whole and carefully built from “counting all” towards “counting on”. 

To do this, we placed the starting number in one bowl and then asked Olivia to add the second number to it. For example, she would have 5 in the bowl to begin with and would be asked to add 3 more. She was very confident at counting the 5 beforehand to ensure she had the correct amount in the bowl to begin with and was also confident in collecting the 3 cubes she needed to add on.

However, we found that when she added the second part to the bowl and was counting the whole, she was counting some of the cubes twice. 

So, at this point, we introduced a second lipped bowl that she transferred the two parts into when adding them together to find the whole. This gave real clarity that the two parts were combining to give the whole and reduced errors. 

Building towards independence

One question that we kept asking was, “Have you scanned your bowl?” We were finding that Olivia was telling us all the counters had been moved and she was finished but we would find one counter hiding in the original bowl, so she had to be continuously reminded to scan the bowl to ensure it was completely empty.

This became a question that Olivia is beginning to ask herself and developed meta-cognition towards becoming independent.  Through using this method of the bowls, it did not take long until she was secure with her numbers up to 10 and adding within 10.

Building efficiency though connecting understanding

The next step in the progression was to develop understanding of addition beyond 10 and to connect this to place value understanding of the unit of 10.  This required a shift of resources, using base ten equipment and regrouping when we got to ten.  We knew that we had to build on from what was secure and that plenty of repetition would be needed so we used a game to support this – Race to 100. 

The game is modelled on the HFL Education: ESSENTIALmaths YouTube channel and is one that I had already used successfully with other children as a high value intervention as well as within the teaching progression for place value and mental calculations. 

I knew that the gaming element supported motivation, frequent practice and focused teaching but also knew that some adaptations would need to be made. 

We created a board with brailed labels of ‘ones’ and ‘tens’ and a thin strip down the middle in order to separate the two groups by touch. This provided a working space and supported the development of place value understanding of ones and tens.

 

 

Keeping focus on the learning

When we started playing the game, we used an adapted raised dice to indicate the number of ones to be collected.  Each time the dice was rolled, Olivia was able to collect the ones and add these to the part that was already known.  This was familiar.

 

 

Importantly, I stopped her when she got to 10.  At this point, I carefully explained that we could regroup 10 ones for a tens stick. I guided her to feel the tens stick so she felt the 10 dents within the stick and understood that you could place 10 ones on top and they would be the same length as a tens stick. We repeated this a few times and every time we got to 10, we regrouped and discussed what was happening.

Building learning in small steps

Once Olivia was comfortable with regrouping 10 ones for a ten, we moved on to bridging over 10. This became quite confusing, and it took a while for her to grasp the concept. We brought out the lipped bowls and rolled the dice; every time she went above 10, we stopped and spoke about the regrouping.

Although she understood that 10 ones could be regrouped for a tens stick, it took a while for her to understand that she could still have ones left over after regrouping as well. The way we got over this was by removing the ten ones that we regrouped for a ten stick and getting her to scan to feel how many ones were left in the bowl.

Once she had counted how many were left, I had planned for us to then count on from 10. This was not the case though. Instead of Olivia remembering the tens stick had a value of ten, she counted it as 1. It took careful explanation, alongside feeling the resources to check and repetition to move the learning forward. 

We repeated the process several times where we bridged over 10 and it took a few sessions for her to remember that the tens stick has the value of ten rather than the value of 1 so she needed to count on from ten. When we then got to 20, we took our time to ensure that she understood that two tens sticks carried the value of 20 rather than 2. However, after this concept was secure, moving on came a lot quicker for her as we worked up the number system.

Building efficiency though developing fact recall

To reduce reliance on counting and to build efficiency, we knew that it was important to support development of fact recall and particularly number bonds to 10.  To teach this, we used a tactile tens frame. We started off by allowing Olivia time to feel and explore the tens frame so she understood that there were 10 spaces on it. 

 

 

We repeatedly used magnetic counters on the tens frame and would place a few on and ask Olivia how many more we would need to count to ten. For this, she had to scan to feel the empty spaces.  At the start, a lot of guidance was needed for her to scan systematically across the tens frame as she was counting the empty spaces twice or missing a few.

To challenge her, we then began to place the counters on the tens frame in a random pattern so she would have to feel for the magnets and then feel for the spaces.

We did have to make sure the magnets were strong as Olivia can be very heavy handed and at times ended up moving the magnets as she scanned around. Again, we repeated this weekly for roughly a term and a half and she is now secure on the recall of her number bonds to ten.

Using key questions

One thing I have noticed that has had to change in my teaching is the language I use for questioning. We regularly ask Olivia, “Are you sure?” when she is giving an answer as a prompt to remind her to look back and see if she has worked it out correctly. Unlike most of the class who can see their answer in front of them when using concrete resources, Olivia can’t, so needed to be taught to regularly go back and check she had counted everything.

Adapting provision based on observation to best meet pupil needs

Through observation and working closely with Olivia’s 1:1 support and the Visual Impairment team, we came to a decision to slow the lessons down and reduce the time of her lessons to 40 minutes. This ensured we focused on the scanning aspects so that was not rushed, as well as identifying how tiring maths lessons were for her and acknowledging that she could not keep her concentration for much longer due to the amount going on within the lesson.

We have also made a conscious decision to regularly introduce new language throughout lessons.  After a few times of the word or phrase being spoken by the adult in the lesson, Olivia can pick it up and begin to use it, although this is still a ‘work in progress’ as she does need reminding quite a bit to do this.

Reflecting on what has been learnt and successes

This year has been an excellent experience and a fantastic learning opportunity for me to teach someone who is visually impaired.  It has taught me many things that I will continue to use to support my teaching. The learning journey Olivia has been on throughout the year has been lovely to watch and it has been amazing to see her confidence in maths grow. As well as this year teaching me a lot of new things about teaching, it has also helped the whole class; their use of language while explaining has come along well as they know they need to explain their answer in enough detail so that the child who is visually impaired understands their answer.

I am excited to see where the next stage of Olivia’s learning takes us as a team.  I look forward to continuing to support her understanding of maths as well as expanding my understanding of strategies of teaching for someone who is visually impaired.

 

 

Providing high quality practical experiences that build on children’s interests linked to the world around them can provide enriching learning opportunities that will support learning across all areas of the EYFS curriculum as well as improving children’s final outcomes in the Early Years Foundation Stage Profile (EYFSP).

 

As we navigate our way through the start of a new academic year, a year since the revised Early Years Foundations Stage statutory framework was applied, now is the perfect time to review and adapt your curriculum, making sure that it provides an inclusive, ambitious and broad and balanced offer for your new cohort of children.

So what is a broad and balanced curriculum?

Put simply, a broad and balanced curriculum provides children in the Early Years Foundation Stage (EYFS) with the life skills and knowledge they need, provided in a holistic, play centred approach, that will equip them to grow up into well rounded individuals. With increasing pressures around assessment and early reading in the EYFS, in some cases, schools and settings are narrowing their curriculum. Here’s where we’re missing a trick…. why not expand our holistic curriculums and use areas of learning such as ‘Understanding the World’ as inspiration to drive your curriculum to enable broad and balanced opportunities to meet the needs of all the children in your cohort as well as fuelling learning across all the other areas of the curriculum. In doing this, children’s learning will not only be supported across all areas of the EYFS curriculum, but we’ll also be expanding children’s cultural capital.

 

 

‘The EYFS’s educational programmes provide the framework for the curriculum. It is up to schools to decide how to expand, extend and broaden these. It is for schools to decide what guidance they choose to use when developing and shaping their curriculums.’ (Ofsted Guidance, The EYFS in schools, July 2022).

Since the revised EYFS statutory framework, the educational programme of ‘Understanding the World’ has changed the Early Learning Goals (ELG’s) to:

• past and present
• people, culture and communities and,
• the natural world

Understanding the world is all about supporting children to make sense of the physical world around them as well as the community they live in. It’s about increasing children’s awareness of their locality as well as developing an appreciation for important members of society such as police officers and nurses. Understanding the world now has clear alignment to early reading clearing stating in the educational programme that understanding the world is about, ‘listening to a broad selection of stories, non-fiction, rhymes and poems will foster…understanding of our culturally, socially, technologically and ecologically diverse world. As well as building important knowledge, this extends…familiarity with words that support understanding across domains. Enriching and widening children’s vocabulary will support later reading comprehension.’

 

 

So how do we use 'understanding the world' to inspire a broad and balanced curriculum?

There are some simple yet effective ways to link ‘understanding the world’ throughout your curriculum to help maximise opportunities for children to engage them in purposeful and real-life practical experiences that will contribute to a holistic curriculum:

1. use high quality books (fiction and non-fiction) as well as poems and nursery rhymes from varying cultures as hooks to excite children about specific topics. This will not only engage children into new learning but will also introduce children to new vocabulary to promote their communication and language skills
2. sudit your learning environment, both indoors and outdoors, to ensure you have effective resources to enable children to explore and investigate how and why things work, where children can test out their ideas of what will happen if they do a particular thing, enjoy problem solving and learn about action and consequences
3. invite important people from your local community to share their experiences, for example, why not invite parents in to share information about their jobs or a visitor from a local place of worship.
4. embrace every opportunity to make use of your local environment, for example, local parks, forests or lakes and even historic buildings or places of worship
5. embrace nature in your setting and be sure to provide natural resources (and even living things) in your provision to provide practical hands-on experiences to evoke children’s senses. Understanding and language development
6. add enhancements to your continuous provision which promote curiosity, awe and wonder, for example, an interesting historical artefact in a curiosity cube which might trigger children to talk about what they have observed using newly introduced vocabulary and provide opportunities for children to record what they see using nearby writing implements on offer

 

 

Providing high quality practical experiences that build on children’s interests linked to the world around them can provide enriching learning opportunities that will support learning across all areas of the EYFS curriculum as well as improving children’s final outcomes in the Early Years Foundation Stage Profile (EYFSP).

 

Why this blog?  Why now?  The main trigger for this blog is that my three favourite reading experiences so far this year have come from a trinity of beautifully crafted novellas.  First came The Blue Book of Nebo by Manon Stefan Ros, an English translation from the original Welsh, and suitable for YA+ readers. I have to thank Jo Bowers, Reviews Editor for Just Imagine for this very welcome recommendation. Then, also thanks to Jo, came Katya Balen’s Birdsong.  I won’t get into how special that book is here, I wax lyrical in this review for Just Imagine: Birdsong — Just Imagine. Finally, in late summer, came a more grown up read: Claire Keegan’s Foster.  This novella is expanded from the original short story published by the New Yorker. It’s so deeply good that I urge you to read it. A profoundly human book.  Not for the first time, I have Mary Roche to thank for a brilliant recommendation. Forgive me if draw on a cliché: each of the above was small and perfectly formed. I thought why not a new “small is beautiful when it comes to reading” kind of blog.  It wouldn’t be my first.

I hope you don’t mind if I briefly rewind back to January 2021 and this blog on the power of short stories in the primary classroom. In that blog, I made a case for including a rich seam of short stories as part of the reading journey our children make through the primary phases. I want to now extend that argument for the inclusion of novellas, or shorter novels. I’ll provide some further rationale and then a range of recommendations that span the phases. Before I do, I just want to repeat some of the most pertinent points made in that blog. I go into the topic in greater depth there. In short though, the following points make a fair stab of distilling those earlier arguments:

• the time constraints of terms and timetables – incorporating shorter reads varies the rhythms of the reading year.  Please don’t think this comes at the expense of longer reads; my suggestions are complementary
• the satisfaction of experiencing, together, a complete narrative within a reasonably short space of time – pretty much all of the suggestions below could be comfortably read aloud in the space of one or two weeks.  In the earlier blog on short stories I expand on this notion of completeness (or perfection if we can briefly get a bit Latinate).  I’m backed up there by no-less than Graham Greene in making that case.  Go and check out his pearls of wisdom
• bringing shorter reads into the reading diet extends the scope for increasing the range and diversity of voices and perspectives shared across the year – this has social and reading-into-writing benefits
• shorter fiction, much like poetry, when done well tends can often make each word and line of prose seem to count for more

 

 

I’ve been meaning to write a blog along these lines for some time now, ever since reading the very special Corey’s Rock, a collaboration between Sita Brahmachari & Jane Ray. That pairing alone should be sufficient reason for getting hold of the book. It’s beautiful across line, length, and image and perhaps most especially in how those words and images interplay. If you do need further persuasion, you could always read this review that I wrote for Just Imagine. As I say, it’s a very special book. I would explore it with classes from year 4 upwards – not because the content is necessarily unsuitable for younger children, but some of the nuance and interplay of word and image might be most fully appreciated by older children.

 

 

Since then, I’ve enjoyed a rich range of novellas both suitable for children to read, and suitable for reading aloud to children. Favourites include The Poet’s Dog by MacLachlan; The Runaways by Ulf Stark with the warm illustrations of Kitty Crowther; A Story Like the Wind by Gill Lewis, with beautiful illustrations from Jo Weaver; and the gently heart-breaking Captain Rosalie by Timothée De Fombelle, with illustrations by Isabelle Arsenault.  Each have offered rich reading and some wonderful opportunities for further supporting deep thoughtfulness and complex discussion.

One of the most interesting set of lessons came from a (very) slow read of the first few pages of Story Like the Wind.  Quite simply, this teaching sequence involved pausing at the end of each section across the opening pages and - much like an approach suggested by George Saunders in his wonderful exploration of Russian short stories, A swim in a Pond in in the Rain – allowing time to discuss the developing story.   I asked children to tell me what they knew as more and more was revealed and the situation and characters took shape. Each page requires plenty of mental joinery. There is much scope to be misdirected, requiring the reader to recalibrate as they move from section to section. Picking our way carefully through such an artfully constructed book offered a hyper-rich chance to carry out some very deep thinking as meanings unfolded. A Story Like the Wind also shares another key strength with all of the books mentioned so far: rich characterisation and interplay between characters that goes well beyond surface level detail or simple plot mechanics. I can’t afford to branch off into a significant and substantial tangent, but this quality of richness in relation to the lives presented in the book is vitally important in developing empathetic readers – and that matters more than we sometimes realise.  It matters so much more. If you would like to know more on the cognitive and social benefits of working with high quality books that support or develop empathy, you might like to listen to this podcast that I recorded with my colleague Marie-Clare Kelly.

To wrap up, I’ve gathered together a relatively condensed list of some of my favourite shorter reads over the past decade or so.  In keeping with the themes of this blog, time was short when I was putting this together and so it is a short list as it stands.

It’s very far from complete – there will be classic and more recent titles missed out altogether.  We’d love to hear your recommendations so do please share them with us on Twitter @HertsEnglish.

Well, for now at least that’s me signing off.  It’s been quite a journey since my then-colleague Rachel Rayner and I first suggested we begin blogging as an organisation.  I’ll miss contributing but I shall certainly look forward to reading more of the team’s output.  Thanks for reading and long may it continue.

 

When I searched ‘problem-solving skills’ online, a list appeared in which the top eight search results were articles about how to develop these skills written by career development companies and job advertising agencies. Why is this?

Clearly, problem-solving is a crucial life skill.

So how do we teach these skills to our young learners in primary school?

Often, when working with teachers and leaders to analyse outcomes from diagnostic or statutory tests, the outcomes show that children are more confident and accurate in solving arithmetical calculations (think SATs paper 1 questions) than they are at interpreting and solving reasoning problems (think SATs paper 2).

This blog will focus on some specific problem-solving skills that will enable pupils to access and solve reasoning questions (as in the KS1 SATs paper 2) by the end of Key Stage 1. But of course, they are more widely applicable.

I will use Question 13 from the 2022 KS1 SATs paper 2 (reasoning) to exemplify this teaching approach.

 

 

Step 1: Direct pupil focus

The purpose of this first step is to reduce anxiety and potential information overload. We want pupils to focus on the structure of the problem before rushing to find a solution.

To do this…

• remove ‘the maths’
• remove ‘the question’
• ask… What do you notice?

 

 

Children may discuss what they can see in pairs, in small groups or as a class. They may benefit from sentence starters such as…

• I can see…
• I have noticed…

These observations may be simple and that is fine. We want to get children engaged and talking.

They may say:

• I can see 3 pencils
• I have noticed a triangle

Step 2: Refine pupil thinking

To do this…

• provide a list of key vocabulary
• expect pupils to articulate their thoughts in full sentences
• ask pupils to listen to others to see if they can add more details or be even more precise

 

 

Now they may say:

• I can see that the shape has 3 sides. It’s a triangle
• I have noticed that there are 3 pencils laying end to end between two vertices

The reference to the 3 sides and 3 pencils is important as it should spark thinking for use later in the problem-solving process.

Step 3: Build on what they know

To do this…

• reveal information from the question bit by bit
• after each reveal, ask the pupils, ‘What do you know now?’
• ask pupils to suggest any additions to the vocabulary list

 

 

Children may discuss what they know now in pairs, in small groups or as a class. They may benefit from sentence starters such as…

• I think that…
• I know that…
• if… then…

They may say:

• I know that 3 pencils will fit along each side because all the sides are equal in length
• if there were 3 pencils along each side, then there would be 9 pencils altogether

Don’t worry at this point if children come up with suggestions that answer the question that will be revealed later. This is a positive thing!

It means the children are tuning in to information within the correct domain and making connections between shape and other areas of mathematics.

Step 4: Consider ‘the question’

To do this…

• BEFORE revealing the question, ask pupils, ‘What could the question be?’

This allows you as the teacher to assess whether the pupils are considering the structure of the problem.

 

 

In this example, are they coming up with questions that involve equal groups, for example?

If a child came up with a question such as, ‘How many pencils would we have if we took one away?’ this can of course still be valued (and answered) but it would indicate that the mathematical domain in which the child is thinking is not one that this picture would naturally allude to.

This information can be considered within class teaching or in rehearsal time going forward.

Step 5: Reveal ‘the question’

 

 

To do this…

• ask children to read the question aloud. Perhaps read it aloud as the teacher and then ask children to repeat it back.
• ensure children understand all of the words within the question and link this to the model and vocabulary list if needed.

Step 6: Represent the problem

To do this…

• ssk the children, ‘How could we draw the problem?’
• ssk the children to compare their drawings to a partner’s. Can they see where each part of the problem is shown? Can they explain their drawing or model to someone else?
• support children to make connections

 

 

As Gill Shearsby-Fox says in her blog about the importance of valuing pictorial recording,

‘We must make time and space for these opportunities and not over-scaffold children’s mathematical thinking with worksheets or prescribed representations, or else maths will become what ‘painting by numbers’ is to art. It might create a lovely picture but can be completed without thought or understanding and isn’t retained or remembered.’

Children may draw:

 

A picture based directly on the image provided showing a continuation of what has been drawn already.

 

A picture of the pencils, removed from the original image, in 3 equal groups of 3.

 

An iconic representation of the pencils. The circles have a 1:1 correspondence with the number of pencils and in this case, are laid out in an array.

 

A symbolic representation using conventional symbols (digits) to represent each quantity of pencils. This part whole model clearly shows the 3 groups of 3.

 

Step 7: Find the answer

To do this,

• ask children to identify on their drawing or model where the answer is shown
• ask, ‘Is there an operation needed?’

 

 

Children may use the operations:

• 3 + 3 + 3 = 9
• 3 x 3 = 9
  While the multiplication fact is not within the coverage of the KS1 curriculum, this may be a known fact for some children.

Ask children to check that they can see the 3 + 3 + 3 within their drawing. Can they see it on someone else’s drawing? Does it look the same? Does it matter?

Step 8: Check the answer makes sense

To do this…

• consider all the information the pupils used while problem-solving (the image, the vocabulary provided, the key words in the question, any models or drawings)
• ask the children to complete the sentence, ‘The answer is … because …’

 

 

They may say:

• the answer is 9 pencils because 3 pencils fit along each side and there are 3 sides. 3 plus 3 plus 3 equals 9
• the answer is 9 pencils because 3 equal groups of 3 make 9 altogether

Developing independence in solving problems

What we would like to see over time is pupils developing more and more independence in using skills and ideas from these steps to solve problems themselves.

When planning a sequence of teaching and learning, refer to the SATs papers for questions that it would be opportune to drop in, either in the way outlined above, as a teaching opportunity, or as an independent or paired discussion task to allow assessment of how pupils tackle them.

This will also provide crucial information about which of the steps the children tend to find the trickiest. Is it articulating what they notice in full sentences? Is it drawing a model to support with choosing an operation? Or is it something else?

Whatever the sticking point, this can form the focus of teaching going forward.

There are plenty of past papers from which to choose questions and these can be accessed here:

• Key stage 1 tests: 2022 mathematics test materials
• Key stage 1 tests: 2019 mathematics test materials
• Key stage 1 tests: 2018 mathematics test materials
• Key stage 1 tests: 2017 mathematics test materials

Further reading

What do we mean by ‘pictorial’ in the CPA approach?

 

End of Key Stage 1 - mathematics assessment toolkit

The HFL Education ‘End of Key Stage 1 - mathematics assessment toolkit’ provides Year 2 teachers and subject leaders with a suite of resources and tools to identify the strengths and areas of development through detailed question level analysis following the completion of a set of practice or statutory SATs papers.

 

 

Accompanying the analysis spreadsheets, documents and tracking tools is a digital guidance video that explains each of the resources and how to use them.

End of Key Stage 1 mathematics assessment toolkit

References

• Department for Education (2021) Development Matters: Non-statutory curriculum guidance for the early years foundation stage. Available at: https://www.gov.uk/government/publications/development-matters--2 (Accessed: 25 August 2022).
• 2022 Key Stage 1 mathematics paper 2: reasoning
  Contains material developed by the Standards and Testing Agency for 2022 national curriculum assessments and licenced under Open Government Licence v3.0

 

I don’t think that we can write a blog series about the 2022 KS2 SATs without firstly acknowledging the disruption to the last 3 years of education which has been vast and varied. However, no matter whether you agree or disagree that the assessments took place this year, the fact is that they did. So, what can we learn from them?

In our first blog in the series, we explored the similarities between the 2022 and previous arithmetic papers with particular comparisons to 2019. In this blog, we will switch our focus to the differences. Finally, in the third blog of the series we will consider the reasoning papers.

I also think that it is really important to remind ourselves that this blog is not just for Year 6 teachers – this is a KS2 assessment at the end of the children’s primary school journey and so all teachers are involved!

Quick domain and year group comparison

Before we dive into key differences we have noted as a maths team, let us just touch on some of the similarities between the 2019 and 2022 arithmetic papers in terms of the domain and year group coverage as shown in the mark schemes.

As detailed in the first blog, the domain coverage remains much the same with the majority of marks shared between calculations and fractions, decimals and percentages (although as detailed in the previous blog, we should note the ‘hidden’ importance of place value understanding). With regards to year group coverage, the picture looks roughly the same across the two years as shown in the tables below:

 

 

In these tables, the primary reference from the mark schemes has been used. The total of 40 refers to the number of marks in the paper with the four 2-mark questions being attributed to Year 6 calculations.

These are referenced in the mark scheme as 6C7a (multiply multi-digit numbers up to 4 digits by a two-digit whole number using the formal written method of long multiplication) and 6C7b (divide numbers up to 4 digits by a two digit whole number using the formal written method of long division, and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context).  

It is useful to note these similarities as it may be assumed that the types of questions asked will be largely the same which is fair to say, and it could be argued that the paper follows a very similar procedure in terms of the writing but in this blog, we will explore some of the more subtle differences and consider their implications.

A tricky opener?

Let’s start at the beginning with the very first question. Historically, the first question, or perhaps the first few questions, have been relatively comfortable for many of the children to access with questions such as:

 

 

Here is this year’s (2022) question which could be argued is a fairly tricky opener:

 

 

How do you do yours?

How did your children tackle this? I wonder how many children may have relied on a formal written method here but made the following errors:

• lined up the place value columns incorrectly given that one number is 4-digit and the other two are 3-digit?
• lined the columns up correctly however when calculating, made errors when adding three 1-digit numbers?
• or made calculating errors when needing to deal with the regroups required in the ones, tens and hundreds columns?

 

 

It would be interesting to use similar questions with classes this year to explore the calculation strategies that the children are choosing to use.

When adding 5 ones, 1 one and 9 ones, do they recognise the complements to 10 and then add 5 more?

Or perhaps when adding 5 tens, 0 tens and 4 tens, do they notice that this could be calculated by doubling 4 tens and adding 1 more ten (and then the regrouped ten from the ones column of course)?

Or perhaps they recognise that if adding the two 3-digit numbers, this could be rebalanced from 501 + 649 to 500 + 650; subtracting 1 from 501 and adding 1 to 649 to keep the sum equal.

1,150 could then be added to 6,155 – perhaps with the children rebalancing again to 1,100 and 6,205 by adding and subtracting 5 tens.

Some questions to consider could be:

• are the children over reliant on formal written methods and if so, do they use these accurately?
• do children have a ‘toolkit’ of strategies and choose these appropriately depending on the numbers at hand?
• is this ‘toolkit’ of strategies built up across the primary phase and revisited often so that children are confident with strategies?
• how often are children given opportunities to use multiple strategies to solve a calculation and then assess efficient and inefficient methods?
• how fluently can children add and subtract 1-digit numbers? Might strategies such as complements to 10, think or make 10, rebalancing, and doubles and near doubles be worth revisiting?

Equal shmequal?

The next difference worth noting is around the concept of the equals sign. As we know from much of our work with teachers and children, when the equals sign is in a less familiar position – perhaps the start of the calculation rather than the end – that this can cause problems.

Why?

Because the children don’t have a secure understanding of the role of the equals sign and what it actually means.

 

 

Having said this, in 2019, the QLA (question level analysis) recorded that the questions above had an average correct response rate of 94% and 93% so not only did the children cope with the fact that the equals sign is at the start of the calculation, they had accurate methods to solve the calculations. It may well be worth comparing how this year’s cohort got on with the following 2 questions:

 

 

Arguably, the calculations needed here should be well within in the grasp of Year 6 children, using their place value knowledge and base facts to solve question 7 and then perhaps a formal method of short multiplication for question 15 (Year 4 content). The shift here is to understanding the role of the equals sign and tackling the division and multiplication calculations which may be operations that children feel less confident with.

If some children are unsure about the role of the equals sign, perhaps only seeing it as meaning ‘the answer’, it would be worth specific exploration of this using equipment such as pan balances and Cuisenaire rods.

For example, start with a fact that the children are confident with and a question such as …… = 2 + 5 and allow children to explore using the rods. Which rod is needed to balance the scales?

Recordings or descriptions could be in the form of:

• 7 = 2 + 5
• 7 is the same as 2 + 5 or
• 7 is equivalent to 2 + 5.

This could then be extended to ….. = 2 x 5 with the children placing 2 lots of the rod worth 5 in one side of the balance and then finding the rod or rods that will balance the scales. …… = 2 x 5 can then be recorded as: 10 = 2 x 5 and 10 is equal to 2 groups of 5 etc.

Once this understanding is secure, this could be extended to division; again using facts that the children are familiar with.

It is often very useful for the children to rehearse saying aloud the calculation and using the word ‘something’ in place of an ‘answer’ box or missing number. For example,

‘Something is equal to 240 divided by 8 so 240 divided by 8 is equal to something’.

Some questions to consider could be:

• how secure is the children’s understanding of the equals sign? Do they have the misconception that = means ‘the answer’ or can they articulate that = means equivalent, the same as or draw comparisons with a balance?  
• did most of the children attempt these questions or were they put off by the fact that they involve multiplication and division?
• would the children cope better with these questions had they involved addition and subtraction and if so, what does this mean about the rehearsal time provided for the children across Key Stage 2?  

Of zero importance

What do each of the following calculations have in common?

 

Those of you who know the papers well may have noticed that these are three of the 2-mark questions. But our focus here is that all of these questions involve 0 as a place holder - another subtle shift in difficulty.

0 is hard to deal with, especially when found within more complex multiplication and division calculations.

These questions aren’t the only ones that involve 0.

 

 

I wonder how many children had the age-old common misconception that 0 x 989 = 989.

If children made these same mistakes in questions 19 and 33, this would cause more than one calculation error and loss of both marks, even if using the formal method.

Throughout questions 19 and 33, the children need to deal with place holders, not only when they are multiplying by the ones and then tens, but also remembering that when multiplying by the 8 tens for example, that this is 8 tens and not 8 ones and so although 8 x 7 = 56 is a useful base fact, it is actually 80 x 7 = 420.

How many times do we see children omitting the 0 when multiplying by the tens digit and not truly thinking about the place value? Often it is the children who may remember the process – multiply by the 3 then multiply by the 8 – who do not have secure understanding when multiplying by the tens digit.  

The zero is perhaps less problematic in the dividend in question 29. However, when subtracting 292 (4 groups of 73) from 306, hopefully the children do not swap the digits around to 9 – 0 and instead see that it is 30 hundreds subtract 29 hundreds leaving 1 hundred.

What may be trickier is that children will need to consider the fact that they need to firstly regroup 3 thousands into 30 hundreds, and then 306 tens before then dividing this by 73. Do they record these place holders at the start of their quotient to help them to keep track that 306 tens divided by 73 is 4 with 14 tens remaining?

Some questions to consider could be:

• do children really understand the effect of multiplying by 0? Can they demonstrate with drawings or models how 0 multiplied by any number will always result in the product of 0 by comparing this to multiplying by 1. For example, do they say ‘1 group of 989 is 989 so 0 groups, or no groups of 989 is 0 or nothing!’
• are children secure when multiplying by tens and hundreds digits? Are they able to articulate that it is 8 tens multiplied by 7 ones and 8 tens multiplied by 6 hundreds for example.
• are children given opportunities to deal with place holders in different positions in complex multiplication and division calculations? For example, are they presented in divisors and dividends? Are they needed in different positions in the quotients? Are questions written carefully so that all of these opportunities arise?

The only way is long division…

Let’s turn our attention to long division as our final difference.

In the mark scheme, children are able to gain a mark if they use the formal methods of either short or long division to solve appropriate questions – in the case of 2022, this is for questions 17 and 29.

 

 

Children are often encouraged to use these methods for these types of calculations as the mark scheme states that, ‘If the answer is incorrect, award ONE mark for the formal method of division with no more than ONE arithmetic error’.

Those of you who have had a lot of experience with the KS2 assessments are likely to know that in the past, all divisors (the number that we are dividing by) used for the 2-mark division questions have been prime numbers.

For example, divisors in the past have been 23 and 97 (2018) and 37 and 83 (2019).

However, this year, the divisor of 21 was used in question 17 – a composite number.

This opens the potential to solve this calculation using knowledge of factors and so potentially making this a more manageable calculation.

• if dividing 672 by 3 first, both 6 hundreds and 72 tens are divisible by 3 perhaps using base facts or knowledge of the distributive law?

  For example, regrouping 72 into 60 and 12. 672 divided by 3 is 224 which could then be divided by 7 (3 x 7 = 21 – the divisor) to give 32.

 

 

• if dividing by 7 first, 67 tens divided by 7 is a manageable calculation using the knowledge that 63 divided by 7 is 9. This would then leave a remaining 42 ones which is a multiple of 7.

  672 divided by 7 is 96 which can then be divided by 3 to give 32.

 

 

In the examples above, you will see that formal methods of division have still been used as a step in solving the original calculation, but these have been simplified by working with the individual factors in turn as divisors instead of 21.

To caveat this, had the children used a method other than a formal method of division and made 1 calculation error, they would not have been awarded a mark for their working out.

It could also be argued that using long division for this calculation (21 is quite a friendly number to multiply after all) using the factors complicates the method.

However, this question nicely highlights that multiple strategies could be used to reach the answer and their efficiency may change from child to child.

It also highlights that when children are rehearsing division methods, all methods should be explored and celebrated. In fact, for those who are very fluent with methods for division, having a formal method banned in a lesson could be more challenging and encourage flexibility and creativity.

Of course, when time is pressured, such as in the actual sitting of SATs papers or using them as a formal practice in readiness, children should be encouraged to use their most efficient and accurate methods.

Some questions to consider could be:

• what does the progression of division methods look like across key stage 1 and key stage 2 in your school?
• are children given opportunities to solve calculations in multiple ways and are calculations written to allow multiple methods e.g., using a prime number as a divisor?
• are different calculation methods shared and celebrated?

As mentioned in the previous blog, this series of blogs has been written before the QLA (question level analysis) is available and so it will be interesting to compare how your children did against national data especially where there has been a change in the way questions have been presented and subtle shifts in complexity.

If you have a chance to have a look at your data, you may want to use the ‘questions to consider’ throughout both blogs to consider implications for teaching and rehearsal, such as:

• checking foundational understanding by tracking back to simpler examples and
• ensuring variation in the types and presentation of questions that children are exposed to and explore.

Year 6 SATs analysis toolkit

The ‘Year 6 SATs analysis toolkit’ provides teachers and subject leaders with a suite of resources and analysis tools to identify specific areas of learning strength and development for pupils and classes when using any past SATs papers as practice (2016-2022).

Accompanying the analysis spreadsheets, documents and progress tracker is a digital guidance video that explains each of the resources and how to use them.

Included with HfL PA Plus subscription and available to purchase from:

Mathematics - Year 6 SATs analysis toolkit

References

• Mathematics test framework: National curriculum tests from 2016 for test developers
• 2017 Key Stage 2 mathematics paper 1: arithmetic
• 2018 Key Stage 2 mathematics paper 1: arithmetic
• 2019 Key Stage 2 mathematics paper 1: arithmetic
• 2022 Key Stage 2 mathematics paper 1: arithmetic
• 2022 Key stage 2 mathematics test mark schemes

Contains material developed by the Standards and Testing Agency for 2016, 2017, 2018, 2019 and 2022 national curriculum assessments and licensed under Open Government Licence v3.0.

 

I don’t think that we can write a blog series about the 2022 KS2 SATs without firstly acknowledging the disruption to the last 3 years of education which has been vast and varied. However, no matter whether you agree or disagree that the assessments took place this year, the fact is that they did. So, what can we learn from them?

In our first blog in the series, we explored the similarities between the 2022 and previous arithmetic papers with particular comparisons to 2019. In this blog, we will switch our focus to the differences. Finally, in the third blog of the series we will consider the reasoning papers.

I also think that it is really important to remind ourselves that this blog is not just for Year 6 teachers – this is a KS2 assessment at the end of the children’s primary school journey and so all teachers are involved!

Quick domain and year group comparison

Before we dive into key differences we have noted as a maths team, let us just touch on some of the similarities between the 2019 and 2022 arithmetic papers in terms of the domain and year group coverage as shown in the mark schemes.

As detailed in the first blog, the domain coverage remains much the same with the majority of marks shared between calculations and fractions, decimals and percentages (although as detailed in the previous blog, we should note the ‘hidden’ importance of place value understanding). With regards to year group coverage, the picture looks roughly the same across the two years as shown in the tables below:

 

 

In these tables, the primary reference from the mark schemes has been used. The total of 40 refers to the number of marks in the paper with the four 2-mark questions being attributed to Year 6 calculations.

These are referenced in the mark scheme as 6C7a (multiply multi-digit numbers up to 4 digits by a two-digit whole number using the formal written method of long multiplication) and 6C7b (divide numbers up to 4 digits by a two digit whole number using the formal written method of long division, and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context).  

It is useful to note these similarities as it may be assumed that the types of questions asked will be largely the same which is fair to say, and it could be argued that the paper follows a very similar procedure in terms of the writing but in this blog, we will explore some of the more subtle differences and consider their implications.

A tricky opener?

Let’s start at the beginning with the very first question. Historically, the first question, or perhaps the first few questions, have been relatively comfortable for many of the children to access with questions such as:

 

 

Here is this year’s (2022) question which could be argued is a fairly tricky opener:

 

 

How do you do yours?

How did your children tackle this? I wonder how many children may have relied on a formal written method here but made the following errors:

• lined up the place value columns incorrectly given that one number is 4-digit and the other two are 3-digit?
• lined the columns up correctly however when calculating, made errors when adding three 1-digit numbers?
• or made calculating errors when needing to deal with the regroups required in the ones, tens and hundreds columns?

 

 

It would be interesting to use similar questions with classes this year to explore the calculation strategies that the children are choosing to use.

When adding 5 ones, 1 one and 9 ones, do they recognise the complements to 10 and then add 5 more?

Or perhaps when adding 5 tens, 0 tens and 4 tens, do they notice that this could be calculated by doubling 4 tens and adding 1 more ten (and then the regrouped ten from the ones column of course)?

Or perhaps they recognise that if adding the two 3-digit numbers, this could be rebalanced from 501 + 649 to 500 + 650; subtracting 1 from 501 and adding 1 to 649 to keep the sum equal.

1,150 could then be added to 6,155 – perhaps with the children rebalancing again to 1,100 and 6,205 by adding and subtracting 5 tens.

Some questions to consider could be:

• are the children over reliant on formal written methods and if so, do they use these accurately?
• do children have a ‘toolkit’ of strategies and choose these appropriately depending on the numbers at hand?
• is this ‘toolkit’ of strategies built up across the primary phase and revisited often so that children are confident with strategies?
• how often are children given opportunities to use multiple strategies to solve a calculation and then assess efficient and inefficient methods?
• how fluently can children add and subtract 1-digit numbers? Might strategies such as complements to 10, think or make 10, rebalancing, and doubles and near doubles be worth revisiting?

Equal shmequal?

The next difference worth noting is around the concept of the equals sign. As we know from much of our work with teachers and children, when the equals sign is in a less familiar position – perhaps the start of the calculation rather than the end – that this can cause problems.

Why?

Because the children don’t have a secure understanding of the role of the equals sign and what it actually means.

 

 

Having said this, in 2019, the QLA (question level analysis) recorded that the questions above had an average correct response rate of 94% and 93% so not only did the children cope with the fact that the equals sign is at the start of the calculation, they had accurate methods to solve the calculations. It may well be worth comparing how this year’s cohort got on with the following 2 questions:

 

 

Arguably, the calculations needed here should be well within in the grasp of Year 6 children, using their place value knowledge and base facts to solve question 7 and then perhaps a formal method of short multiplication for question 15 (Year 4 content). The shift here is to understanding the role of the equals sign and tackling the division and multiplication calculations which may be operations that children feel less confident with.

If some children are unsure about the role of the equals sign, perhaps only seeing it as meaning ‘the answer’, it would be worth specific exploration of this using equipment such as pan balances and Cuisenaire rods.

For example, start with a fact that the children are confident with and a question such as …… = 2 + 5 and allow children to explore using the rods. Which rod is needed to balance the scales?

Recordings or descriptions could be in the form of:

• 7 = 2 + 5
• 7 is the same as 2 + 5 or
• 7 is equivalent to 2 + 5.

This could then be extended to ….. = 2 x 5 with the children placing 2 lots of the rod worth 5 in one side of the balance and then finding the rod or rods that will balance the scales. …… = 2 x 5 can then be recorded as: 10 = 2 x 5 and 10 is equal to 2 groups of 5 etc.

Once this understanding is secure, this could be extended to division; again using facts that the children are familiar with.

It is often very useful for the children to rehearse saying aloud the calculation and using the word ‘something’ in place of an ‘answer’ box or missing number. For example,

‘Something is equal to 240 divided by 8 so 240 divided by 8 is equal to something’.

Some questions to consider could be:

• how secure is the children’s understanding of the equals sign? Do they have the misconception that = means ‘the answer’ or can they articulate that = means equivalent, the same as or draw comparisons with a balance?  
• did most of the children attempt these questions or were they put off by the fact that they involve multiplication and division?
• would the children cope better with these questions had they involved addition and subtraction and if so, what does this mean about the rehearsal time provided for the children across Key Stage 2?  

Of zero importance

What do each of the following calculations have in common?

 

Those of you who know the papers well may have noticed that these are three of the 2-mark questions. But our focus here is that all of these questions involve 0 as a place holder - another subtle shift in difficulty.

0 is hard to deal with, especially when found within more complex multiplication and division calculations.

These questions aren’t the only ones that involve 0.

 

 

I wonder how many children had the age-old common misconception that 0 x 989 = 989.

If children made these same mistakes in questions 19 and 33, this would cause more than one calculation error and loss of both marks, even if using the formal method.

Throughout questions 19 and 33, the children need to deal with place holders, not only when they are multiplying by the ones and then tens, but also remembering that when multiplying by the 8 tens for example, that this is 8 tens and not 8 ones and so although 8 x 7 = 56 is a useful base fact, it is actually 80 x 7 = 420.

How many times do we see children omitting the 0 when multiplying by the tens digit and not truly thinking about the place value? Often it is the children who may remember the process – multiply by the 3 then multiply by the 8 – who do not have secure understanding when multiplying by the tens digit.  

The zero is perhaps less problematic in the dividend in question 29. However, when subtracting 292 (4 groups of 73) from 306, hopefully the children do not swap the digits around to 9 – 0 and instead see that it is 30 hundreds subtract 29 hundreds leaving 1 hundred.

What may be trickier is that children will need to consider the fact that they need to firstly regroup 3 thousands into 30 hundreds, and then 306 tens before then dividing this by 73. Do they record these place holders at the start of their quotient to help them to keep track that 306 tens divided by 73 is 4 with 14 tens remaining?

Some questions to consider could be:

• do children really understand the effect of multiplying by 0? Can they demonstrate with drawings or models how 0 multiplied by any number will always result in the product of 0 by comparing this to multiplying by 1. For example, do they say ‘1 group of 989 is 989 so 0 groups, or no groups of 989 is 0 or nothing!’
• are children secure when multiplying by tens and hundreds digits? Are they able to articulate that it is 8 tens multiplied by 7 ones and 8 tens multiplied by 6 hundreds for example.
• are children given opportunities to deal with place holders in different positions in complex multiplication and division calculations? For example, are they presented in divisors and dividends?
• are they needed in different positions in the quotients? Are questions written carefully so that all of these opportunities arise?

The only way is long division…

Let’s turn our attention to long division as our final difference.

In the mark scheme, children are able to gain a mark if they use the formal methods of either short or long division to solve appropriate questions – in the case of 2022, this is for questions 17 and 29.

 

 

Children are often encouraged to use these methods for these types of calculations as the mark scheme states that, ‘If the answer is incorrect, award ONE mark for the formal method of division with no more than ONE arithmetic error’.

Those of you who have had a lot of experience with the KS2 assessments are likely to know that in the past, all divisors (the number that we are dividing by) used for the 2-mark division questions have been prime numbers.

For example, divisors in the past have been 23 and 97 (2018) and 37 and 83 (2019).

However, this year, the divisor of 21 was used in question 17 – a composite number.

This opens the potential to solve this calculation using knowledge of factors and so potentially making this a more manageable calculation.

• if dividing 672 by 3 first, both 6 hundreds and 72 tens are divisible by 3 perhaps using base facts or knowledge of the distributive law?

  For example, regrouping 72 into 60 and 12. 672 divided by 3 is 224 which could then be divided by 7 (3 x 7 = 21 – the divisor) to give 32.

 

 

• if dividing by 7 first, 67 tens divided by 7 is a manageable calculation using the knowledge that 63 divided by 7 is 9. This would then leave a remaining 42 ones which is a multiple of 7.

  672 divided by 7 is 96 which can then be divided by 3 to give 32.

 

 

In the examples above, you will see that formal methods of division have still been used as a step in solving the original calculation, but these have been simplified by working with the individual factors in turn as divisors instead of 21.

To caveat this, had the children used a method other than a formal method of division and made 1 calculation error, they would not have been awarded a mark for their working out.

It could also be argued that using long division for this calculation (21 is quite a friendly number to multiply after all) using the factors complicates the method.

However, this question nicely highlights that multiple strategies could be used to reach the answer and their efficiency may change from child to child.

It also highlights that when children are rehearsing division methods, all methods should be explored and celebrated. In fact, for those who are very fluent with methods for division, having a formal method banned in a lesson could be more challenging and encourage flexibility and creativity.

Of course, when time is pressured, such as in the actual sitting of SATs papers or using them as a formal practice in readiness, children should be encouraged to use their most efficient and accurate methods.

Some questions to consider could be:

• what does the progression of division methods look like across key stage 1 and key stage 2 in your school?
• are children given opportunities to solve calculations in multiple ways and are calculations written to allow multiple methods e.g., using a prime number as a divisor?
• are different calculation methods shared and celebrated?

As mentioned in the previous blog, this series of blogs has been written before the QLA (question level analysis) is available and so it will be interesting to compare how your children did against national data especially where there has been a change in the way questions have been presented and subtle shifts in complexity.

If you have a chance to have a look at your data, you may want to use the ‘questions to consider’ throughout both blogs to consider implications for teaching and rehearsal, such as:

• checking foundational understanding by tracking back to simpler examples and
• ensuring variation in the types and presentation of questions that children are exposed to and explore.

Year 6 SATs analysis toolkit

The ‘Year 6 SATs analysis toolkit’ provides teachers and subject leaders with a suite of resources and analysis tools to identify specific areas of learning strength and development for pupils and classes when using any past SATs papers as practice (2016-2022).

Accompanying the analysis spreadsheets, documents and progress tracker is a digital guidance video that explains each of the resources and how to use them.

Included with HFL Education PA Plus subscription and available to purchase from:

Mathematics - Year 6 SATs analysis toolkit

References

• Mathematics test framework: National curriculum tests from 2016 for test developers
• 2017 Key Stage 2 mathematics paper 1: arithmetic
• 2018 Key Stage 2 mathematics paper 1: arithmetic
• 2019 Key Stage 2 mathematics paper 1: arithmetic
• 2022 Key Stage 2 mathematics paper 1: arithmetic
• 2022 Key stage 2 mathematics test mark schemes

Contains material developed by the Standards and Testing Agency for 2016, 2017, 2018, 2019 and 2022 national curriculum assessments and licensed under Open Government Licence v3.0.

 

In 2011, the pupil premium grant (PPG) was introduced to help close the attainment gap between disadvantaged children and their peers. The funding is available for children in Reception to Year 11 and there is a set criterion for the eligibility for this funding found in the Pupil Premium overview:

• children who are eligible for free school meals, or have been eligible in the past 6 years
• children who have been adopted from care or have left care
• children who are looked after by the local authority

Service pupil premium (SPP) is additional funding for schools, but it is not based on disadvantage. Children are eligible for this funding if they have parent/carer:

• serving in HM Forces
• retired on a pension from the Ministry of Defence

Whilst this funding is a positive step in supporting disadvantaged and vulnerable children, there are a few challenges to identifying exactly who is eligible when starting Reception. These challenges include families’ lack of knowledge about the funding, later applications made due to children receiving universal free school meals or declining to apply through personal embarrassment.  There are a few strategies that schools have implemented to help gather this information sensitively to ensure all eligible children are able to receive funding sooner.

Transition procedures

It is important to gather as much information about children and their families prior to staring school. The transition level of need tool (TLoNT) should help you to identify vulnerable children to help prioritise an enhanced transition process, however, all children need effective transition procedures in place to enable them to settle into school.

• contact with feeder settings – ensure that you make time to visit the new children at their feeder setting in the summer term (PVI/school nursery/childminder). If this is a challenge, make time to have a conversation with each child’s key person remotely (telephone/video call) to find out about the child’s interests and potential barriers to learning. Use these discussions to find out whether the child is in receipt of Early Years Pupil Premium (EYPP) funding as this may be an indicator of eligibility for PPG funding. Parents/carers will still need to apply for PPG funding even if the child is receiving EYPP funding.
• parents and carers – include the PPG application form in your admissions pack as many parents/carers like to ensure they have everything prepared for their child to start school. Alternatively, take the forms with you to home visits or when having 1:1 conversations prior to the children starting. This way, you can talk it through with parents/carers or even help fill them in with them if required. There are occasions, where through home visits, practitioners will identify a vulnerability for the family, however, this might not indicate that they are eligible for PPG funding. These families still need to be monitored to ensure that should they become disadvantaged, the school are able to provide them with appropriate support.
• school events – use induction meetings to provide families with information on how the school can support them with home learning and relevant support services if required. Make families feel welcome through informal meetings or workshops to help build positive relationships. This could also be an opportunity to provide them with time to complete relevant paperwork. If you have asked families to complete documents digitally, this might be a challenge. Consider providing laptops/computers/tablets for parents/carers to access in school.

The Supporting Smooth Transitions toolkit has a wealth of information on how to enhance transition processes for children and families including resources that can be sent directly to them during the summer holidays which is when many families are most vulnerable.

 

 

Communication

Review your communication procedures to ensure that they are accessible to all families. Consider conducting a survey to find out the most effect method of communication for your families.

• emails
• texts
• school digital platforms
• social media
• telephone/video calls

If there are challenges with families understanding the communication coming from the school, this may hinder information being gathered in a timely manner. Ensure that all communication is inclusive of the families in your school community. Do you use simple, concise sentences? Do you use images or icons to enhance your messages? Have you considered recording voice notes/messages for parents/carers to be able to listen to? Can your messages be easily translated into various languages spoken at home?

Take time to review how parents/carers can communicate with the school. It should be just as effective as how the school communicates with home.

 

 

Initiatives

It could be worth offering incentives to families in return for the information required to identify eligibility such as a free…

• book bag
• school jumper
• P.E. kit

This also enables all children, including those identified as disadvantaged, to have appropriate school clothing/equipment. Whilst this type of incentive requires an initial outlay it is worth considering the long term gains. Once a child has been identified as eligible for PPG funding they will be eligible for the rest of their time in the Primary phase, irrespective of changing circumstances.

NB A child in Reception will attract £1, 385 for the Reception year and a further possible £8,310 by the end of KS2. This is a considerable amount of money to improve outcomes for that individual.

 

 

Roles and responsibilities

Whilst it is everyone’s responsibility to ensure positive outcomes for every child, it is best practice to ensure that a member of staff’s role is to monitor and evaluate the impact of funding on outcomes for disadvantaged children. One part of this role should be co-ordinating the identification of eligible families. PPG funding can be used to fund this member of staff to spend an allocated amount of time per week/term to oversee this. It would be beneficial if this person’s role included…

• attending welcome meetings and parent consultations
• contacting parents/carers either face-to-face or by telephone
• liaising with external professionals

By implementing a range of robust strategies, you will be able to identify children eligible for funding. It is then that you can consider how to allocate the funding to improve outcomes for individuals and begin to address social inequality.

For further guidance on a supporting vulnerable and disadvantaged children look at:

Resource: Making the difference - Early Years Toolkit 2021 edition - Supporting disadvantaged and vulnerable children

 

This blog has been lurking, unwritten, at the back of my mind for a while.

The danger with writing about ‘back to basics’ is that it becomes patronising, and this is not my aim. As teachers, we are a highly skilled and dedicated profession; my aim is certainly not to tell anyone what they already know.

The aim is to confirm, support and reflect on what we believe and know has impact on learning in the classroom. So that as you read, you nod along to yourself, safe in the knowledge that you already balance these suggestions appropriately, for the learning happening in your classroom or school. Like when you listen to a great speaker at an event, and they resonate with you in a way that both affirms your beliefs and strengthens your sense of purpose.

My focus is primary mathematics.

The role I play involves working with a range of schools, supporting subject leaders and teachers, modelling teaching, helping with planning, supporting learning walks, and leading staff meetings, among many other things. As a class teacher at heart, my driver is making both teaching and leadership manageable and effective, helping deep learning to happen in schools.  

After the first partial school closures in the spring/summer of 2020, what struck me was the incredible way teachers and schools so quickly adapted; to manage risk, to allow teaching and learning to happen, to create safe environments. Some choices felt like necessary measures to reduce the risk of transmission, such as children in rows where they might normally sit around tables in groups. Or giving children their own sets of stationary equipment to avoid the need to share. We were all anxious: we were worried about the risks, the impact on learning and the impact on children’s well-being.

However you feel about where we are now, 2 years on, there is definitely a feeling that things are gradually relaxing where possible and appropriate. You might be more likely to see children sat in groups again or sharing glue sticks. There might be a shared pot of pens and pencils rather than individual equipment packs. Some children in the youngest year groups may have now had their first experience of assemblies in the hall. We are finding ways to bring back our routines and systems (and holding onto some of the ones we like and have worked well for us more recently).

There has been a huge impact on children’s collective learning and well-being from the disruption of the last 2 years. We notice children have many gaps. Some of these are more social skills and self-regulation based; some more academic learning gaps.

We know we need to scaffold and track back, re-teach or pre-teach, to find and close those gaps.

So, how can we ensure our teaching is as effective as possible, particularly within this current scenario? How do we teach in a way that promotes learning opportunities, filling gaps but also aiming forwards?

Here are my thoughts, with a focus on primary maths and on the gaps within curriculum learning, but with many overlaps both across subjects and key stages.

1. identify the key learning. Where does this fit within the journey of the curriculum?
2. take a step back. What might need pre-teaching or reactivating, before children are ready to build towards the pitch you are aiming for?
3. consider your first example, model or question; make it accessible to all and then build on it.
4. model everything; the process, thinking, visuals and talk.
5. engage everyone; through the way you ask questions and call on responses.
6. allow sufficient practice and rehearsal time.
7. continually assess for learning. Does it look, feel, and sound like everyone is with you?

These thoughts in more detail:

1. identify the key learning. What is it you are trying to teach and what do you want the children to learn (to know or be able to do)? Where does this fit within the journey of the curriculum - what should have come before this and where is it going next?

2. take a step back. What might need pre-teaching or reactivating, before children are ready to build towards the pitch you are aiming for? Before launching into the learning, anticipate whether children will have the steps in place that should have come before this learning. There may be key points to re-cap or vocabulary to rehearse.

   We can sometimes be guilty of simply following our long-term plan. Whatever our long-term plan suggests, I would still ask myself; Why this? Why now? Pausing to consider what this learning builds from and builds onto. The ‘building from’ will also tell me what I need to pre-teach or reactivate, knowing that there may be gaps, insecure learning, or misconceptions.

   For example, in Year 5, I might be due to teach ‘reading timetables’ and ‘calculating with time’. Before I start, I will most likely need to check that children are secure with reading digital clocks in both 12 and 24-hour time. The learning about conversion between analogue and digital usually happens within Year 4. Reading time to the nearest minute on an analogue clock usually happens within Year 3. So, for the Year 5 learning to be successful, I need to check on this pathway, filling gaps as we go, to build solid foundations for the new learning. If I consider these aspects 2-3 weeks before the main input comes up, I could plot some of the pre-teaching and reactivation work into short maths fluency sessions, starters, or classroom routines, so that children rehearse reading an analogue clock, looking at digital 12 and 24-hour time and using the language of time (60 minutes in an hour, 24 hours in a day), before we embark on ‘reading timetables’ and ‘calculating with time’. Or I can plan in time for this at the start of the sequence of learning.

   Here is a set of matching cards to explore analogue and digital, am/pm, 12 and 24-hour time. This is from our ESSENTIALmaths planning and resources for Year 5. It’s from the first part of the sequence that focuses on reading timetables and calculating with time:
    

   

    

3. consider your first example, model or question; make it accessible to all and then build on it. Where do you need to start so that everyone understands and can follow what you are modelling?

   Using the same example as previous, ‘reading timetables’ and ‘calculating with time’, I need to select the right first example; something with a manageable amount of information. Is my focus reading timetable? How can I help the children focus on the reading and interpreting of the information?

   Again, this example comes from our ESSENTIALmaths planning and resources for Year 5.

    

   

4. model everything; the process, thinking, visuals and talk. Say and show what you are doing, how and why. Write it and draw it for pupils to see. Enable the children to ‘play along’ with the modelling. Mix modelling with questioning when the children are ready.

   This could be as simple as being really explicit about which part of the example you are explaining, pointing to and drawing everyone’s attention to the part you are thinking about. In maths, we talk about using the CPA approach (concrete, pictorial, abstract); ensuring that the physical manipulatives, pictures/diagrams and the abstract representations work together to build a deeper understanding.

5. engage everyone; through the way you ask questions and call on responses (talk partners, rough books, white boards, shared counting, choral responses and many other ways).

   For me, this one is a must. Even if the previous four points are in place, if children are just watching you, occasionally putting their hand up, they may not be truly engaged, and the understanding might not be as deep as you think. A way to allow children to process the learning and for you to assess their understanding is to use strategies such as small whiteboards and/or talk partners regularly. My personal preference is to use both. I want all children fully engaged and participating in the learning.

6. allow sufficient practice and rehearsal time. This enables children to process, develop fluency and confidence, develop understanding, and build memory. We know that when we say a child lacks confidence, we often mean they didn’t have long enough to practice and secure the learning. So, giving rehearsal time is often key for the confidence, fluency, and retention of learning.

7. continually assess for learning. Does it look, feel, and sound like everyone is with you?

   This might be during the input and can be easily done when scanning children’s whiteboards or asking questions. This might be when you are reviewing pupils’ work. The follow up to this would be:

   • what happens for the children who seem less secure?

   • what systems are in place?

Whether you are reading this as a class teacher or a subject leader (or from another school leadership role), you are probably already reflecting on whether this happens within your own classroom or school, the extent to which it happens and whether it is having the impact you want. Are learning gaps being filled gradually?

We started by saying that although this has a ‘back to basics’ heading, the aim is not to just tell you what you know, but to confirm the good practice already happening in classrooms, affirming what we do well but with a focus on ensuring that our efforts are put into the areas most likely to ensure learning happens.

The 7 points above may help to neatly summarise what we hope is happening in all primary maths classrooms, to allow all children to fully access the learning, after what has undoubtedly been a very disrupted time for them in education.

If you’re looking for support with primary maths teaching or subject leadership through in-school or remote consultancy, staff meeting or INSET sessions, please get in touch for further details.

 

As a TLA with HFL Education I have recently supported a Lower Key Stage Two teacher. She was particularly interested in the work of Derek Haylock, which she had studied at university as part of her Initial Teacher Training; and was keen to implement the ideas. As part of the Primary Mathematics Specialist Teacher Programme (MaST) that I attended at Brighton University I had significant experience of carrying out Action Research in classrooms through Case Studies based on the work of Haylock so I was also keen to be involved.

The support began with looking at maths theory linked to the teaching and learning of formal addition. Haylock (2010) asserts that the use of a variety of concrete and pictorial materials when teaching formal methods for addition and subtraction is vital if children are to understand the concepts. He advocates the use of a place value chart combined with a range of manipulatives and discusses the (often misused) terms of ‘carrying’ and ‘exchanging’ which is now more commonly referred to as ‘regrouping’.

This process is also linked to the rationale of allowing children to make connections in their learning. Haylock and Thangata (2007) assert that

‘Making connections in mathematics refers to the process in learning whereby the pupil constructs understanding of mathematical ideas through a growing awareness of relationships between concrete experiences, language, pictures, and mathematical symbols. Understanding and mastery of mathematical material develops through the learner’s organisation of these relationships into networks of connections.’

 

(Adapted from Haylock, D., and Thangata, F. (2007), Key Concepts in Teaching Primary Mathematics, London: Sage p.34.)

 

The teacher and I discussed how these networks can be effectively built through the children communicating their ideas across all situations in a variety of ways that allow them to demonstrate their clear understanding. Recognition of these relationships needs to be facilitated in cyclical ways to allow for both continued consistency of approach and subsequent impact. 

I was keen to implement these ideas in a Year Three class, where common misconceptions were not in the process of carrying out the formal method of addition but were concerned with the children’s explanations (and consequent understanding) of the mathematical processes. This was prevalent within a group of six children (I taught these children in two sessions with the Year Three teacher present).

My rationale for this, in terms of mathematical progression, was guided by the National Curriculum for Mathematics 2014 (NC) statement for Year Three:

‘Add and subtract numbers with up to three digits, using formal written methods of columnar addition and subtraction’

and the Related NC Statements of:

‘recognise the place value of each digit in a three-digit number (hundreds, tens, ones)’ – ‘identify, represent and estimate numbers using different representations’

and

‘add and subtract amounts of money to give change, using both £ and p in practical contexts’.

I also wanted the children to discuss their mathematical work and begin to explain their thinking, e.g., use appropriate mathematical vocabulary to talk about their findings by referring to their written work. My methodological approaches were to both engage in participant observation, interpret the verbal responses and to analyse written responses for conceptual understanding and correct use of the arithmetic operation of formal addition.

Assessment of their previous work saw the children having instrumental understanding (Skemp, 1989) where they have a mechanical, rote or 'learn the rule/method/algorithm' kind of learning but not relational understanding which is a more meaningful learning where the pupils are able to understand the links and relationships which gives mathematics its structure. My aspirations were to use the concrete materials to elicit the latter.

I discussed with the Year Three teacher how Haylock’s (2010) analysis of the terms ‘carrying’ and ‘exchanging’ and their associated confusion for children when carrying out formal methods for addition led to his recommendations for the use of resources where coins and number lines can be used in the exploration of the related place value.

 

 

 

(Haylock, D. (2010), Mathematics Explained for Primary Teachers, 4th edition, London: Sage p.14.)

 

Implementation and analysis

As a preliminary exercise the children used the Base 10 equipment and played the ‘Race to 100’ game from ESSENTIALMaths which is demonstrated by my colleague Gill Shearsby-Fox: Race to 100 (see link for details).

The overarching aim here was for the children to understand the term ‘regrouping’ where, for example, ten ones have the same value as one ten so ten ones can be regrouped as one ten and the ten ones can be exchanged for one ten. As a continuation of the preliminary exercise, I also related the coins to the Base 10 equipment and demonstrated how the ‘ones’ matched the pennies, the tens block matched the ten pence pieces and the hundred block matched the pound coins. I demonstrated that the coins could be exchanged between each other which had the same equivalent value. This involved exchanging ten pennies for a ten pence piece and ten, ten pence pieces for a pound coin. We also included, for example, 13p as 13 pennies exchanged for a ten pence piece and three pennies. The ‘Race to 100’ game was also played using coins.

All the coins were in a ‘bank’ which the children used to complete their regrouping and exchange transactions. The rationale for this was that they could then physically ‘carry’ the Base 10 equipment and the coins across to the next column in the Place Value chart.

The next step was to include the coins in an A3 sized place value chart alongside the Base 10 equipment (see below). 

 

 

Firstly, we placed coins and concrete materials and regrouped them and ‘carried’ them across without making formal calculations e.g. thirteen one pence pieces were placed in the ones column and ten were exchanged in the bank and then carried over to show one ten piece in the tens column and three pennies in the ones column. This was continued with the ten pence pieces and the pounds and with the Base 10 equipment. The children ‘played’ with this idea and constructed their own different amounts. They were then asked to show specific amounts and explain their reasoning. The next stage involved the use of the A3 place value grid to carry out formal addition calculations.  Digits were place in the columns with the coins as headings and the titles of ‘Hundred’, ‘Tens’ and ‘Ones’. The Base 10 equipment was also placed in each column. Another set of digits was placed underneath alongside concrete materials and the children added together the two, three-digit numbers. This was carried out initially without bridging tens or hundreds to show the initial concept. Bridging was then introduced in the ones and tens columns only, followed by another calculation with bridging to one hundred and beyond but not to one thousand (see below).

 

 

This is the result of 152 + 119. The one’s column had eleven ‘ones’ in it. Ten of these were regrouped for a ten pence piece which was carried and is underneath the tens column along with the ten block from the Dienes Apparatus. This was also shown as a written algorithm.

 

 

The children explored this idea before I demonstrated, using the concrete resources, how the number that was regrouped was carried over was put below the calculation line to be added in the next column. This was accompanied by the same formal calculation to show the connections between the formal methods with and without concrete materials. This realisation conforms with Haylock and Thangata’s (2007) ideas for children making networks of connections.

The thought process here was to allow the children to gain relational understanding from progressive steps. They then constructed and answered their own calculations and then they were asked to create calculations that would bridge ten and one hundred, and then answer them. This encompassed Bruner’s (1960) ‘Mode of Representational Thought’ where children need experience of mathematics at the three levels of ‘iconic’ (the Dienes apparatus and the coins), ‘symbolic’ (the calculation as numbers) and ‘enactive’ (manipulation of the concrete materials).

Findings

The impact was dramatic. All the children demonstrated and asserted that they understood the concepts. Their reactions were vociferous with typical 21st Century comments such as: ‘I get it, I SO get it!’, ‘That is sick!’ and ‘Wow, I understand completely!’ They were then asked to write calculations and explain their understanding verbally and in writing. The children took great delight in explaining that the small figure ‘one’ under the calculation was actually a ten or a hundred carried across after it had been exchanged (see below).

 

 

Conclusions and next steps

The specific and progressive implementation of resources based on analysis of maths theory compounded the children’s understanding by giving them a holistic overview. This was evidenced throughout the process and used and applied effectively. The children had clearly made a network of connections in their processes of learning where they constructed understanding of mathematical ideas through a growing awareness of relationships. 

 

(Adapted from Haylock, D., and Thangata, F. (2007), Key Concepts in Teaching Primary Mathematics, London: Sage p.34.)

 

As the graphic above shows, the children should also be able to make the connection between the coins and Place Value counters and reason mathematically to solve a calculation such as this:

 

 

This is planned to be continued with the teaching of zero as a place holder and subtraction for the children to make further connections especially with regard to decomposition and inverse operations. They should also be able to make connections with money and its equivalents and the concept of decimals should be made easily transferable through the children’s enhanced understanding of place value.

Haylock (2010) also asserts that although the National Curriculum for Mathematics (2014) outlines that ‘Calculators should not be used as a substitute for good written and mental arithmetic’, they could be used as an abstract resource especially with regard to the teaching of money. If the children are asked to put ‘one pound and five pence’ into a calculator, it will help to focus their thinking on the underlying mathematical structure of the situation and be able to enter £1.05 and not £1.5 with the latter being a common misconception.   Using the devices in this way as resources utilises them as companions to be included in a network of connections and not alternative methods.

The key point from the exercise is that the manipulation of the concrete resources, based on pedagogical theory related to the effective teaching of primary mathematics, demonstrated the connected understanding for the children who can then move confidently into the abstract and solve calculations with clear understanding.

The Year Three teacher asserted that she recognised the benefits of the both the rationale and the process and aspired to implement it further to continue to enhance her pedagogy.

Other recent related blogs from HFL Education include:

Back to basics in the maths classroom – 7 ways to make learning happen

What do we mean by ‘pictorial’ in the CPA approach?

---

References

Bruner, J. (1964), Towards a Theory of Instruction, London: Belknap Press in Delaney, K. (1992), Teaching mathematics resourcefully, in Gates, P. (Ed), (2001) Issues in Mathematics Teaching. London: Routledge Falmer.

Haylock, D. (2010), Mathematics Explained for Primary Teachers, 4th edition, London: Sage.

Haylock, D., and Thangata, F. (2007), Key Concepts in Teaching Primary Mathematics, London: Sage.

National Curriculum for Mathematics (2014) https://www.gov.uk/government/publications/national-curriculum-in-england-mathematics-programmes-of-study [Accessed 22 September 2022].

Skemp, R. R. (1989), Mathematics in the Primary School, London: Routledge.

UCL Libraries, (2014), http://libguides.usc.edu/content.php?pid=83009&sid=616083

[Accessed 22 September 2022].

 

 

What are your first thoughts when a colleague discloses a mental health issue to you? Is it ‘I don’t know how to respond to this’? If you’re a line manager, do you instantly worry that this disclosure will result in increased sickness absence? Maybe you’d worry about the employee’s ability to do their job? Or do you feel confident and comfortable enough to have an open discussion with them before making any preconceived judgements?  

If your first thought is ‘how best can I support this person?’ – amazing, the chances are you are part of an empathetic workplace that have succeeded in encouraging open discussions around mental illness; your setting is likely to have positive practices that help create an inclusive work climate - which is the goal.   

What can you do to get to that point? Unfortunately, not everyone understands mental health problems. Some people may have misconceptions about what certain diagnoses mean. I personally have struggled with Generalised Anxiety Disorder, Social Anxiety, SAD and PMDD for years. I don’t mind people knowing this now, but it took a long time for me to open up about it to my employers. I’m fortunate that I have a supporting senior leadership team and I hope they’d agree that this diagnosis hasn’t affected my ability to do my job. Them having the knowledge of my mental health issues, along with my Insights Discovery profile - which uses a model of 4 colour energies to help people understand themselves and others - they are fully equipped to understand my preferences and there is no stigma (I’m very ‘cool blue’/’earth green’ for those who are familiar with it!). Unfortunately, stigma and discrimination still exist in some workplaces, and that stigma can negatively affect relationships, work, education and the chance to live a normal life. Something that others often take for granted. Take a moment to think about whether there may be a feeling of prejudice at your setting around mental health disclosures. Recognising and accepting this is key to creating inclusivity. 

 

 

I appreciate that education settings are already doing a huge amount of work in terms of mental health and well-being – does your setting focus as much on staff well-being as it does its pupils well-being? Ideally, speaking about mental health problems should be an intrinsic part of the culture of your setting. Health is not always seen as a strategic enabler that drives performance. But it should be. If we feel well, we can perform better and of course this has a knock-on effect on the success and school experience of your pupils. If someone asked you the question ‘how do you encourage your staff to have open conversations about mental health?’, what would you say? One option for consideration might be the HFL Wellbeing Quality Mark which has a module on Staff Wellbeing.  

Talking about mental health can be difficult but it’s important to note that you don’t need to be an expert to talk about mental health, you are not expected to make a diagnosis or have all the answers. In many ways, it should be approached in the same way you would any other kind of health-related problem – seek specialist input. What you can do is ask questions and be willing to spend time listening to their answer. Imagine if that one question meant your colleague opened up about feeling overwhelmed and, for example, they disclosed to you that during their PPA time there’s a chatterbox who has PPA at the same time and they can’t concentrate so they’re getting further and further behind. Something so easy to resolve but not something they’ve been able to manage or had the confidence to address themselves. I appreciate issues are not always that straight forward but asking simple, open and non-judgmental questions and letting your employee explain in their own words how their mental health problem manifests, the triggers, how it impacts on their work and what support they think they might need, will help. Small changes you can make in your settings can go a long way in supporting someone’s mental health. Mind have some useful resources as a first step  

 

 

Earlier in the year I presented a ‘Managing staff well-being and mental health disclosures’ webinar to a school who wanted a bespoke session for their line managers at one of their inset days and ironically, for days I spent the lead up incredibly anxious and subdued, and after the session I spent days over-thinking perhaps what I should have said, or not said - but that doesn’t mean I can’t do it – I realised after this that I may just have to prepare differently to someone else and accept that any intrusive thoughts and the fatigue that follows will pass. The relationship between our performance and mental health is complex. Some people ask me how I can work in Human Resources when I have social anxiety, but for me it’s easy, there’s a purpose, a focus to the discussions and advice, it’s easy because it’s my job and it’s familiar; but send me to a school reunion with a room full of people I haven’t seen for over 20 years (how much over 20 I won’t disclose!) and I’ll be out of there quicker than you can say “small talk”!  

It is often wrongly assumed that all mental health problems lead to underperformance. It might be that it just helps for your colleagues to know, and it may explain some behaviours. It can feel scary but have, or encourage, that conversation.  

Another great tip is to be aware of what is happening in people’s personal lives as stress outside of work, for example due to illness, bereavement or financial worries might be contributing to them struggling to cope in the workplace. Again, have conversations, communication is key. It might be that you need to seek advice and support yourself. You’re not expected to have all the answers. It might be that you need to make an Occupational Health referral or if relationships have become strained or confrontational, mediation might help. Does your setting have an Employee Assistance Program you can direct employees to? If not, perhaps your setting could consider adopting one.   

 

 

I really like this Equality vs Equity illustration with the bikes, I thought it was a bit different to the one we’re all familiar with illustrating the stools. The supportive measures, the tools we use, look different for different people, there is no one size fits all when it comes to supporting a mental health issue. Traditionally employers have been aiming for equality to reach a more level playing field - what this doesn’t do though is take into account an employees’ physical, mental and emotional needs, which means in reality it continues to deliver an unbalanced end result. The concept of equity is to understand the individual needs of each person – and to offer a different level of support, so that each employee can reach the same outcomes as others. By striving for equity where possible, employers can create inclusive and diverse workplaces where everyone is given equal opportunity to succeed. I urge you to have a think about what this might look like in your setting, with your staffs’ different needs.  

If you notice someone who appears to be struggling, make the first move in encouraging the disclosure of a problem, it could be related to mental ill health. 

If you’re feeling overwhelmed, you have to reach out to somebody. You can’t do it alone. Whether it’s a friend, a colleague, a mental health first aider, a professional – reach out. 

---

HFL HR services subscribers

Employee wellbeing is a key issue that organisations are striving to address to ensure that their employees remain happy and motivated at work, this section provides guidance and useful services that support the process. Our model wellbeing policy, managing stress tools, and wellbeing guidance and resources:

Maintained schools: Wellbeing

Academies/trusts: Wellbeing

HFL Wellbeing Quality Mark

Helping to place health and wellbeing at the heart of the whole school community:

HFL Wellbeing Quality Mark