
As a TLA with HFL Education I have recently supported a Lower Key Stage Two teacher. She was particularly interested in the work of Derek Haylock, which she had studied at university as part of her Initial Teacher Training; and was keen to implement the ideas. As part of the Primary Mathematics Specialist Teacher Programme (MaST) that I attended at Brighton University I had significant experience of carrying out Action Research in classrooms through Case Studies based on the work of Haylock so I was also keen to be involved.
The support began with looking at maths theory linked to the teaching and learning of formal addition. Haylock (2010) asserts that the use of a variety of concrete and pictorial materials when teaching formal methods for addition and subtraction is vital if children are to understand the concepts. He advocates the use of a place value chart combined with a range of manipulatives and discusses the (often misused) terms of ‘carrying’ and ‘exchanging’ which is now more commonly referred to as ‘regrouping’.
This process is also linked to the rationale of allowing children to make connections in their learning. Haylock and Thangata (2007) assert that
‘Making connections in mathematics refers to the process in learning whereby the pupil constructs understanding of mathematical ideas through a growing awareness of relationships between concrete experiences, language, pictures, and mathematical symbols. Understanding and mastery of mathematical material develops through the learner’s organisation of these relationships into networks of connections.’
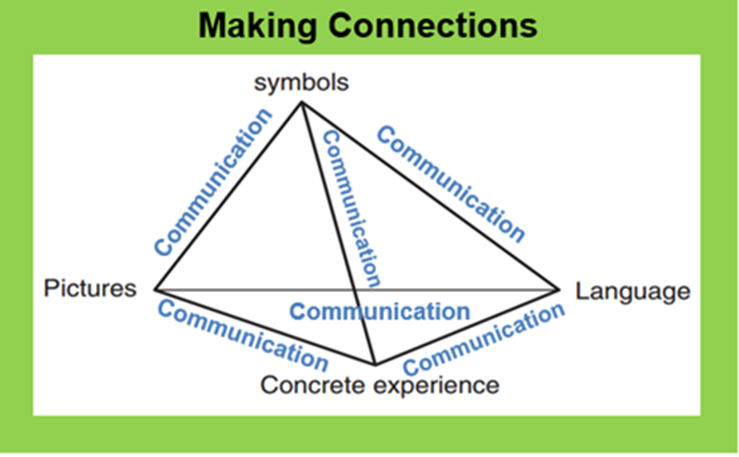
(Adapted from Haylock, D., and Thangata, F. (2007), Key Concepts in Teaching Primary Mathematics, London: Sage p.34.)
The teacher and I discussed how these networks can be effectively built through the children communicating their ideas across all situations in a variety of ways that allow them to demonstrate their clear understanding. Recognition of these relationships needs to be facilitated in cyclical ways to allow for both continued consistency of approach and subsequent impact.
I was keen to implement these ideas in a Year Three class, where common misconceptions were not in the process of carrying out the formal method of addition but were concerned with the children’s explanations (and consequent understanding) of the mathematical processes. This was prevalent within a group of six children (I taught these children in two sessions with the Year Three teacher present).
My rationale for this, in terms of mathematical progression, was guided by the National Curriculum for Mathematics 2014 (NC) statement for Year Three:
‘Add and subtract numbers with up to three digits, using formal written methods of columnar addition and subtraction’
and the Related NC Statements of:
‘recognise the place value of each digit in a three-digit number (hundreds, tens, ones)’ – ‘identify, represent and estimate numbers using different representations’
and
‘add and subtract amounts of money to give change, using both £ and p in practical contexts’.
I also wanted the children to discuss their mathematical work and begin to explain their thinking, e.g., use appropriate mathematical vocabulary to talk about their findings by referring to their written work. My methodological approaches were to both engage in participant observation, interpret the verbal responses and to analyse written responses for conceptual understanding and correct use of the arithmetic operation of formal addition.
Assessment of their previous work saw the children having instrumental understanding (Skemp, 1989) where they have a mechanical, rote or 'learn the rule/method/algorithm' kind of learning but not relational understanding which is a more meaningful learning where the pupils are able to understand the links and relationships which gives mathematics its structure. My aspirations were to use the concrete materials to elicit the latter.
I discussed with the Year Three teacher how Haylock’s (2010) analysis of the terms ‘carrying’ and ‘exchanging’ and their associated confusion for children when carrying out formal methods for addition led to his recommendations for the use of resources where coins and number lines can be used in the exploration of the related place value.
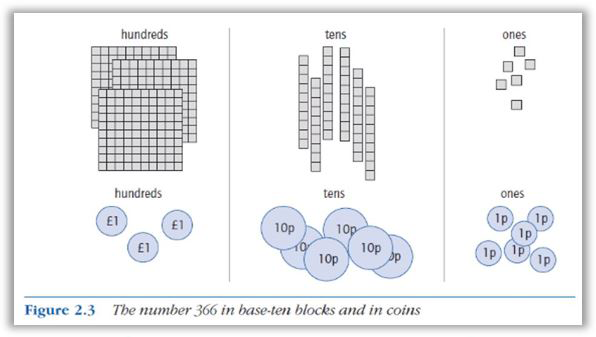

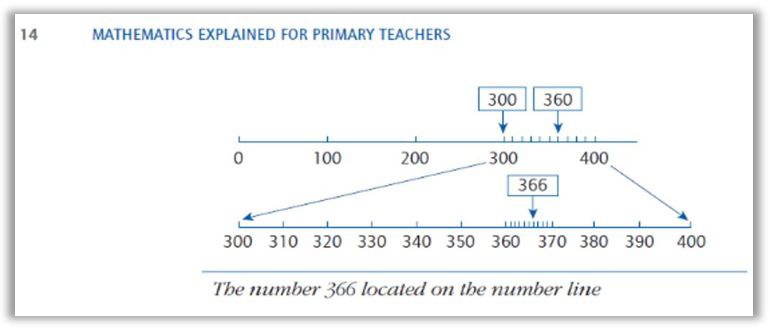
(Haylock, D. (2010), Mathematics Explained for Primary Teachers, 4th edition, London: Sage p.14.)
Implementation and analysis
As a preliminary exercise the children used the Base 10 equipment and played the ‘Race to 100’ game from ESSENTIALMaths which is demonstrated by my colleague Gill Shearsby-Fox: Race to 100 (see link for details).
The overarching aim here was for the children to understand the term ‘regrouping’ where, for example, ten ones have the same value as one ten so ten ones can be regrouped as one ten and the ten ones can be exchanged for one ten. As a continuation of the preliminary exercise, I also related the coins to the Base 10 equipment and demonstrated how the ‘ones’ matched the pennies, the tens block matched the ten pence pieces and the hundred block matched the pound coins. I demonstrated that the coins could be exchanged between each other which had the same equivalent value. This involved exchanging ten pennies for a ten pence piece and ten, ten pence pieces for a pound coin. We also included, for example, 13p as 13 pennies exchanged for a ten pence piece and three pennies. The ‘Race to 100’ game was also played using coins.
All the coins were in a ‘bank’ which the children used to complete their regrouping and exchange transactions. The rationale for this was that they could then physically ‘carry’ the Base 10 equipment and the coins across to the next column in the Place Value chart.
The next step was to include the coins in an A3 sized place value chart alongside the Base 10 equipment (see below).

Firstly, we placed coins and concrete materials and regrouped them and ‘carried’ them across without making formal calculations e.g. thirteen one pence pieces were placed in the ones column and ten were exchanged in the bank and then carried over to show one ten piece in the tens column and three pennies in the ones column. This was continued with the ten pence pieces and the pounds and with the Base 10 equipment. The children ‘played’ with this idea and constructed their own different amounts. They were then asked to show specific amounts and explain their reasoning. The next stage involved the use of the A3 place value grid to carry out formal addition calculations. Digits were place in the columns with the coins as headings and the titles of ‘Hundred’, ‘Tens’ and ‘Ones’. The Base 10 equipment was also placed in each column. Another set of digits was placed underneath alongside concrete materials and the children added together the two, three-digit numbers. This was carried out initially without bridging tens or hundreds to show the initial concept. Bridging was then introduced in the ones and tens columns only, followed by another calculation with bridging to one hundred and beyond but not to one thousand (see below).

This is the result of 152 + 119. The one’s column had eleven ‘ones’ in it. Ten of these were regrouped for a ten pence piece which was carried and is underneath the tens column along with the ten block from the Dienes Apparatus. This was also shown as a written algorithm.
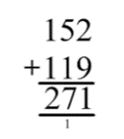
The children explored this idea before I demonstrated, using the concrete resources, how the number that was regrouped was carried over was put below the calculation line to be added in the next column. This was accompanied by the same formal calculation to show the connections between the formal methods with and without concrete materials. This realisation conforms with Haylock and Thangata’s (2007) ideas for children making networks of connections.
The thought process here was to allow the children to gain relational understanding from progressive steps. They then constructed and answered their own calculations and then they were asked to create calculations that would bridge ten and one hundred, and then answer them. This encompassed Bruner’s (1960) ‘Mode of Representational Thought’ where children need experience of mathematics at the three levels of ‘iconic’ (the Dienes apparatus and the coins), ‘symbolic’ (the calculation as numbers) and ‘enactive’ (manipulation of the concrete materials).
Findings
The impact was dramatic. All the children demonstrated and asserted that they understood the concepts. Their reactions were vociferous with typical 21st Century comments such as: ‘I get it, I SO get it!’, ‘That is sick!’ and ‘Wow, I understand completely!’ They were then asked to write calculations and explain their understanding verbally and in writing. The children took great delight in explaining that the small figure ‘one’ under the calculation was actually a ten or a hundred carried across after it had been exchanged (see below).

Conclusions and next steps
The specific and progressive implementation of resources based on analysis of maths theory compounded the children’s understanding by giving them a holistic overview. This was evidenced throughout the process and used and applied effectively. The children had clearly made a network of connections in their processes of learning where they constructed understanding of mathematical ideas through a growing awareness of relationships.
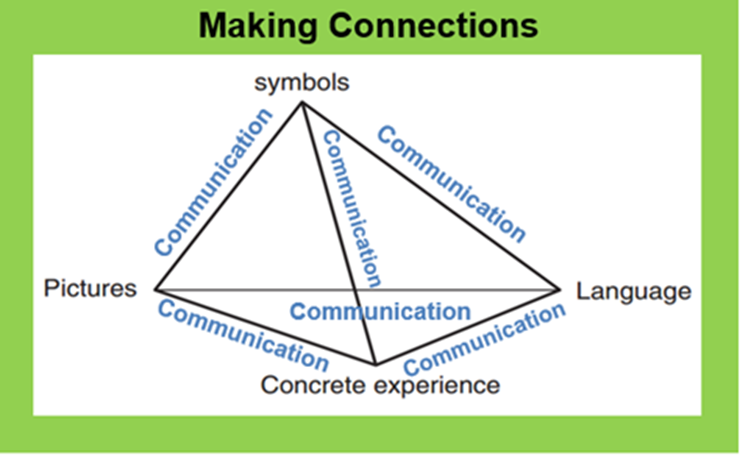
(Adapted from Haylock, D., and Thangata, F. (2007), Key Concepts in Teaching Primary Mathematics, London: Sage p.34.)
As the graphic above shows, the children should also be able to make the connection between the coins and Place Value counters and reason mathematically to solve a calculation such as this:
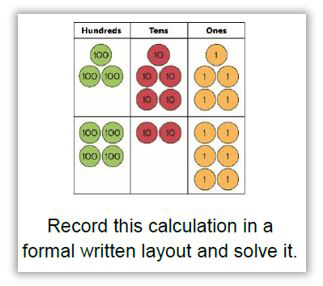
This is planned to be continued with the teaching of zero as a place holder and subtraction for the children to make further connections especially with regard to decomposition and inverse operations. They should also be able to make connections with money and its equivalents and the concept of decimals should be made easily transferable through the children’s enhanced understanding of place value.
Haylock (2010) also asserts that although the National Curriculum for Mathematics (2014) outlines that ‘Calculators should not be used as a substitute for good written and mental arithmetic’, they could be used as an abstract resource especially with regard to the teaching of money. If the children are asked to put ‘one pound and five pence’ into a calculator, it will help to focus their thinking on the underlying mathematical structure of the situation and be able to enter £1.05 and not £1.5 with the latter being a common misconception. Using the devices in this way as resources utilises them as companions to be included in a network of connections and not alternative methods.
The key point from the exercise is that the manipulation of the concrete resources, based on pedagogical theory related to the effective teaching of primary mathematics, demonstrated the connected understanding for the children who can then move confidently into the abstract and solve calculations with clear understanding.
The Year Three teacher asserted that she recognised the benefits of the both the rationale and the process and aspired to implement it further to continue to enhance her pedagogy.
Other recent related blogs from HFL Education include:
Back to basics in the maths classroom – 7 ways to make learning happen
What do we mean by ‘pictorial’ in the CPA approach?
References
Bruner, J. (1964), Towards a Theory of Instruction, London: Belknap Press in Delaney, K. (1992), Teaching mathematics resourcefully, in Gates, P. (Ed), (2001) Issues in Mathematics Teaching. London: Routledge Falmer.
Haylock, D. (2010), Mathematics Explained for Primary Teachers, 4th edition, London: Sage.
Haylock, D., and Thangata, F. (2007), Key Concepts in Teaching Primary Mathematics, London: Sage.
National Curriculum for Mathematics (2014) https://www.gov.uk/government/publications/national-curriculum-in-england-mathematics-programmes-of-study [Accessed 22 September 2022].
Skemp, R. R. (1989), Mathematics in the Primary School, London: Routledge.
UCL Libraries, (2014), http://libguides.usc.edu/content.php?pid=83009&sid=616083
[Accessed 22 September 2022].



