I have noticed that teachers are talking about subitising like it’s going out of fashion and I’m sure this wasn’t even in my vocabulary early in my career. I find children’s learning fascinating and this was an excuse to dig a little deeper.
As Doug Clements said, “Subitizing: What is it? Why teach it?”
He had me hooked in his opening sentence: “Three pictures hang in front of a six month-old child. The first shows two dots, the others show one dot and three dots. The infant hears three drumbeats. Her eyes move to the picture with three dots”.
It turns out scientists have been exploring this for hundreds of years and of course, they disagree.
Some purport that subitising is a necessary pre-cursor to counting – such as Fitzhugh in 1978, who found that while she could find some children able to subitise sets (very young children and very small sets of 1 or 2) without being able to count them, none of them could count any sets that they could not subitise. This led her and many followers to conclude that subitising must come first.
But there are many eminent minds who believe that children use counting in order to develop the skill of subitising and in this camp, you will find our good friends Gelman and Gallistel who have been instrumental to our understanding of counting for many years. Many teachers will tell you that it was only when they read their five principles of counting that they began to understand how number should be taught.
Do you know what? I love a good discussion but I think I am happy to know that subitising and counting are inextricably linked and I want to understand them both to give my children the best chance!
So let’s pick it apart to understand it better:
Breaking it up a little bit, we know that there is ‘perceptual subitising’ and ‘conceptual subitising’ that lay behind the skill.

So this is just “recognising” values and this is what the six month old baby was doing when she moved her eyes to the three dot pattern but we know this only works with small sets, usually up to 4 or 6, unless they are in a very familiar pattern (like dots on a die or a tens frame).

Conceptual subitising, on the other hand, requires arithmetic strategies – recognising smaller values within larger ones – like subsets – and then knowing what to do with those to find the larger total.
So you don’t want one without the other; you need to be able to recognise small values to see them within a larger set and children who cannot subitise conceptually are at a distinct disadvantage in arithmetical processes.
I wanted to think about this and its implications for teaching, because in the end I’m not a scientist; I’m a teacher. Did my provision in the classroom teach conceptual subitising?
Some of you may already be aware of a collaborative project between my colleague and me from the maths team, with members of the early years team, to produce “Essential Foundations for Counting” in which we unpick subitising and what progression looks like for this and 3 other skills:
The criteria that map the progression for each skill takes place across four stages that we decided to call NOTICE, COPY, EXTEND and CREATE because it feels like all learning begins when children start to notice things. We then have the opportunity to deepen their confidence and grow their independence to be creative with what they have learned.
If perceptual subitising is ‘recognising’ then I’m going to want to start with interesting conversations.

Let’s look at 3 in different ways, for a bit of challenge, and to make sure the conservation of number is also growing. Look at these alongside some familiar patterns that they can visualise more easily than three saucepans and then “find” 3.

Of course, the re-modelling of the language is the real teaching here and I’m going to follow it up with…


Knowing that this is just the first step in their progression, I will continue to explore, ask questions and re-model their language to point out matching arrangements when they “copy”. Then ask more provocative questions to encourage the children to “extend” their thinking so that they will begin to recognise smaller amounts within a larger arrangement of marks or objects. I can see that many children will begin to respond to the prompts and will start to show evidence of conceptual subitising in their learning. With enough opportunities for exploration and enough variation in the learning experiences, I feel confident that most of our children in Reception will learn to use their group recognition skills to partition and combine numbers, reaching the “create” stage of the progression and using their conceptual subitising skills to work arithmetically.
We realised just how important this is in our teaching when we devoted a whole booklet to subitising but what practitioners are saying is that they are really only just beginning to see how important this learning is but have found a great freedom in giving it the value it deserves and immersing the children in rich and broad learning opportunities just to talk about values up to 4!
If we allow sufficient time and depth to model and remodel the language of this hugely significant learning, maybe conceptual subitising will look more reachable in Reception.
Those of you familiar with the learning in ESSENTIALmaths for Year 1 will already know that we begin the year with this very learning in the second learning sequence.
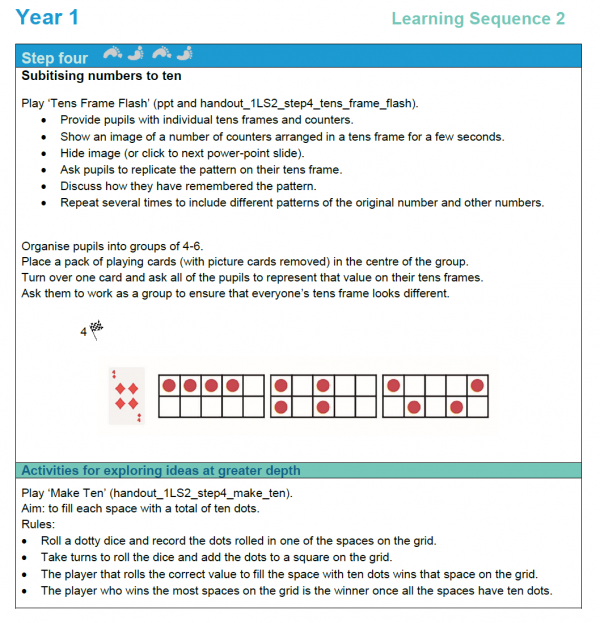
The key concepts for this sequence include the exploration of patterns in numbers through subitising. Initially starting with familiar dot patterns, like those found on dice and playing cards, pupils will begin to see how numbers can be regrouped in different ways but still conserve their value. Using the tens frame provides a structure for this and helps pupils to begin to notice complements to 10.
This year we have published the “missing bridge” - Reception ESSENTIALmaths.

Once again, at the beginning of the Reception ESSENTIALmaths, we explore the perceptual and conceptual subitising. In this first sequence, having recognised values in familiar patterns, children will begin to compare quantities by recognising equivalent and different totals that are not always in familiar patterns. There is a focus on their mathematical language again of course.
The vocabulary of more, less and equal is used to describe quantities they can see and compare.


Clements and Samara explore children’s developmental paths in learning mathematics through learning trajectories where they ask:
- What objectives should we establish?
- Where do we start?
- How do we know where to go next?
- How do we get there?
They track the developmental progression from age 1 to 5 (and beyond) and match it to “instructional tasks” and when you read this you can see that the understanding of the five principles of counting is firmly embedded.
Rochel Gelman and Randy Gallistel introduced the idea of “five separate and distinct principles that children need to understand in order to be proficient counters” in 1978 and I mentioned these at the top of the blog. For any mathematical learning to be meaningful for our children, numbers need to be meaningful and learning to count is hard!
You can crudely categorise the five principles as:
“How to Count”
1. The 1:1 Counting Principle: You say one number and only one number name for each object you count.
2. The Stable-Order Principle: There is a sequence of number names that is universal and will not change.
3. The Cardinality Principle: The last number of the count, when counting objects, labels the total of the set.
“What to Count”
4. The Abstraction Principle: We still count the same way whatever we are counting (the objects could be varied, moving, hidden etc.)
5. The Order-Irrelevance Principle: It doesn’t matter where you start to count from or the order you count the items in, the total of the set will always be the same.
You can see that it’s pretty complex stuff so deep and rich learning experiences are absolutely essential for real understanding. Using number in as many different contexts as possible, counting moving objects, objects that vary, objects that cannot be seen but only heard are just some of the ways we need to explore early mathematical development and the focus is to gain a true understanding of numbers as values in a system that will help you all of your life once you understand it. You can use the system to understand values you have never seen before when it all makes sense.
This is why being a teacher in EYFS is so fascinating, so challenging but so rewarding too. If we can unpick these early developmental stages and understand the conceptual progression that every child needs, we can make the learning so powerful and that will be thrilling. We have tried to share all that we know in the Reception ESSENTIALmaths materials to keep the learning well informed by key mathematical concepts.

Most of our teachers are investing a huge amount of time in this first sequence of the year because of all its hidden complexities and they are able to use the steps to ensure the learning is not rushed. It is so important for children to fully explore numbers up to five – count them, put smaller numbers within five together and take them apart and compare them – before they explore sets to 10 in the same way.
Fully understanding that a whole can be made up of several parts within a set and indeed that smaller parts can be used to make bigger sets (wholes) is also crucial. We learn to create sets, make pictorial representations of sets and visualise them in our minds before we can be truly playful with number. This is why we don’t address numbers greater than 10 until the 13th out of 16 learning sequences.
I think we can pretty safely conclude that this is important stuff and no wonder teachers are talking about subitising. Hey who knew? When you’re seeing dots, there’s nothing wrong. You’re subitising and you’re going to be a brilliant mathematician!
Further reading/research:
You may be interested in a lecture that explores subitising and early learning in number by Doug Clements on YouTube.
There is much more to support you including ideas and resources on his website.
Bibliography
D. Clements (published 1999) “Subitizing: What Is It? Why Teach It?”
Fitzhugh, J. I. (1978). The role of subitizing and counting in the development of the young children’s conception of small numbers Dissertation Abstracts International, 40, 4521B-4522B
D. Clements & J. Sarama (published online July 21, 2010)Learning Trajectories in Early Mathematics – Sequences of Acquisition and Teaching
Gelman, R., & Gallistel, C.R. (1978). The child's understanding of number. Cambridge: Harvard University