
Multiplication and division
By Year 6, children’s understanding of multiplication and division (and recall of facts) should be secure enough to enable them to make use of formal written methods such as long multiplication and long division, applying them within a variety of problem-solving contexts.
The ability to do this relies on many layers of learning and multiplicative understanding. In this blog, I will share ideas and strategies for teaching concepts within multiplication and division, set in the imaginary world of a beautiful picture book.
Teaching multiplication and division with beadstrings
Beadstrings are a useful manipulative to use when exploring equal groups for multiplication and division.
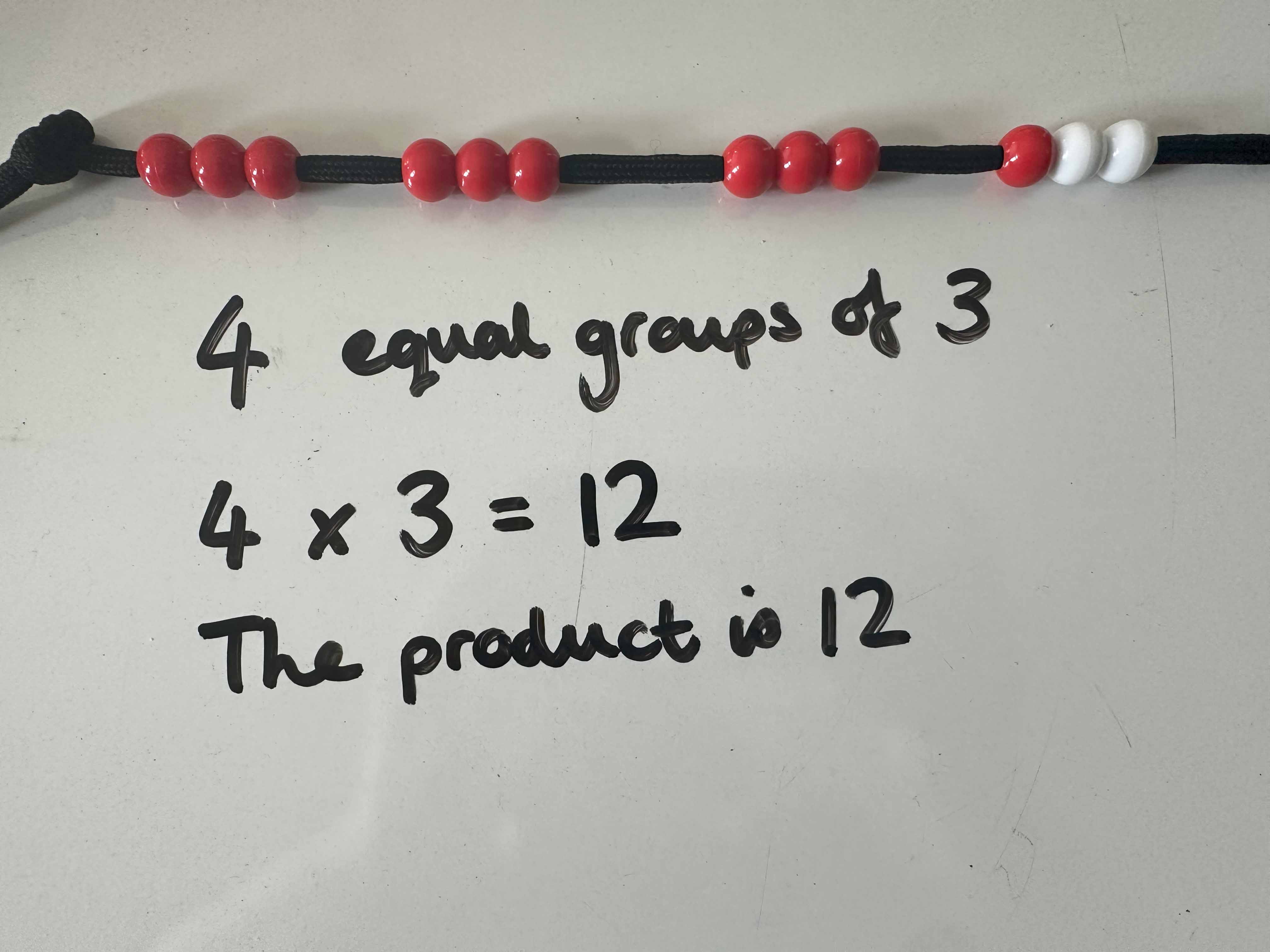
For example, to explore 4 multiplied by 3, equal groups of 3 can be pulled out along the beadstring to show multiples of 3.
The language of ‘equal groups’ and ‘product’ and the formal equation are all connected to the visual representation.
Fact families
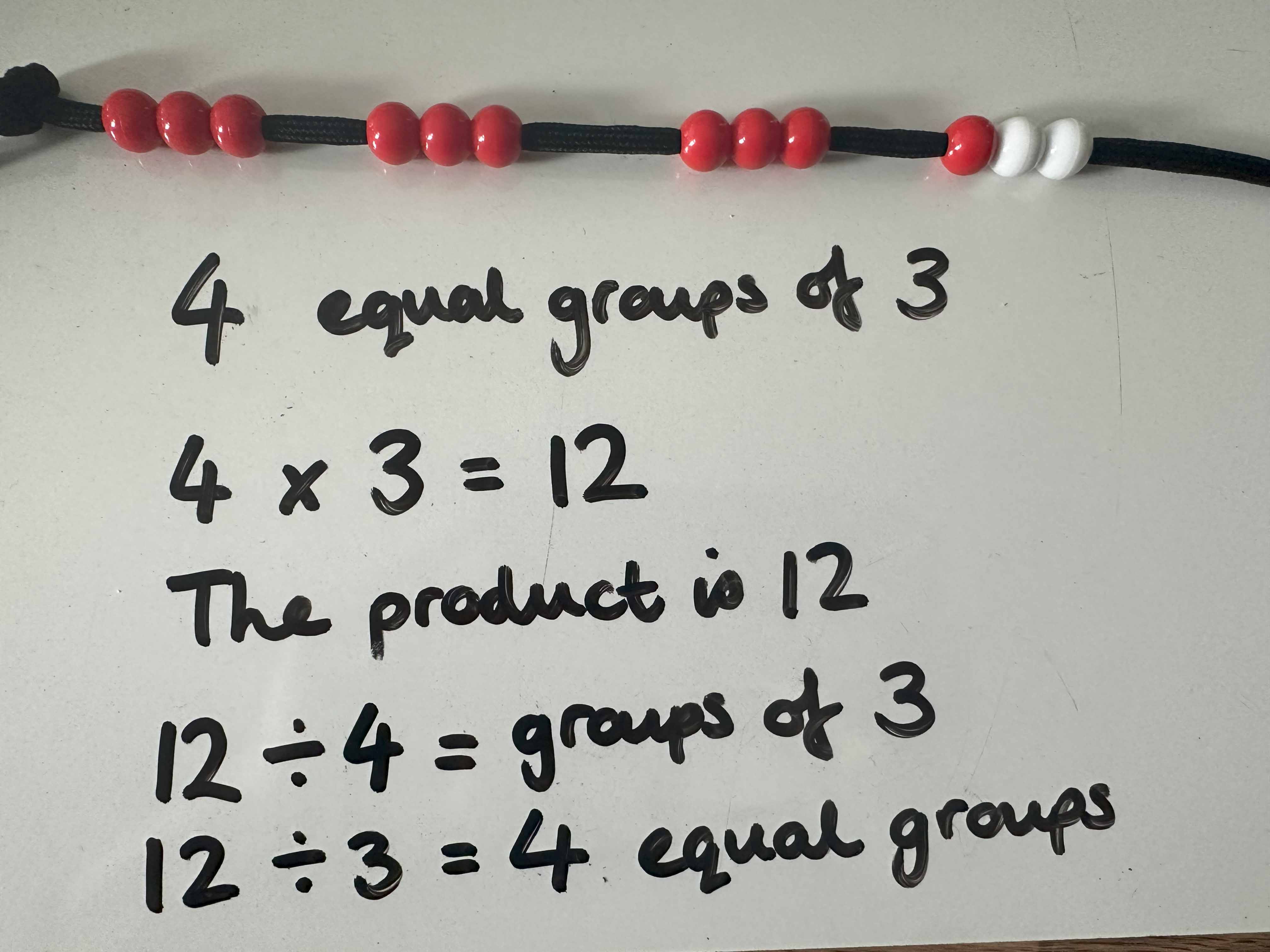
The beadstring is a useful resource for exploring the grouping structure of division and the link to multiplication.
(For exploring the sharing structure, counters or cubes would be more appropriate).
If dividing 12 by 3, we can ‘pull’ out groups of 3 beads to found out how many groups we can make.
The beadstring is a staple in many primary school classrooms. If you are less familiar with them, take a look at this blog to get you started: Step-by-step guide to using the 0-100 bead string from Year 1 to Year 6.
Whole school maths through stories
One hundred ants were singing
And marching in a row.
“We’re going to a picnic!
A hey and a hi dee ho!”
World Book Day is fast approaching and this year, we shine a spotlight on the work of Elinor J Pinczes, and the book, One Hundred Hungry Ants.
More ideas for incorporating maths into World Book Day here: Maths through stories

This wonderful picture book follows the journey of a group of ants on their way to a picnic.
One ant isn’t happy with the speed the ants are travelling and so suggests alternative formations to get them to the picnic quicker!
The book is written with rhyme and repetition and is easily accessible across the primary phase.
Multiplication and division concepts linked to scenarios in this story:
- Equal groups (EYFS and KS1)
- Sharing and grouping (KS1 and KS2)
- Constructing arrays and commutativity (KS1 and LKS2)
- Relationship between multiplication and division facts (KS1 and KS2)
- Factors (Y4 and UKS2)
- Heuristics – build a model, act it out, draw a picture, find all possibilities, solve a simpler but related problem (all phases)
Using a beadstring to support exploration of multiplication and division
Some of the reasons I might use a beadstring to explore this story:
- There are 100 hungry ants and 100 beads on the beadstring!
- Units of 10 are clearly visible and can support skip counting.
- Beadstrings can be easily ‘folded’ to create arrays.
We could use counters or multilink but with larger numbers, this could get messy!
- We can quickly revisit the structure of multiplication and division on the beadstring with lower numbers before exploring the story.
- It’s an easy manipulative to use to support development of heuristics like building a model and drawing a picture.
Teaching ideas for EYFS and KS1 classrooms
Read the story to the children under a visualiser and share the images as the story progresses.

Drawing attention to equal groups by making a model
Draw the children’s attention to the lines / equal groups being formed by the marching ants.
Model and explore this.
For example:


Watch out for children who do not see these lines as equal because of the colours of the beads. Bring their focus back to the value / number of beads in each line.


The beadstrings could be presented with or without the labels as the focus is on the equal groups.
Solve a simpler but related problem
Children could be tasked with a simpler but related problem.
How many different formations could be made by 20 hungry ants?
0-20 beadstrings would be particularly useful here.
For example:


Children could build or act out the problem using other resources such as counters, cubes or themselves!
Children might draw out their formations to show the multiplication.

Further exploration and challenge:
- How will the children know they have found all possible formations?
- Can they prove that a given formation will not work? For example, why can the 20 hungry ants not march in lines of 6?
- Would the ants get to the picnic quicker if they marched in 2 lines/groups of 10 or 10 lines/groups of 2?
Linking multiplication and division – fact families
Use the models and formations drawn out through a simpler but related problem to link multiplication and division calculations. Children could use speaking frames to describe the relationships.
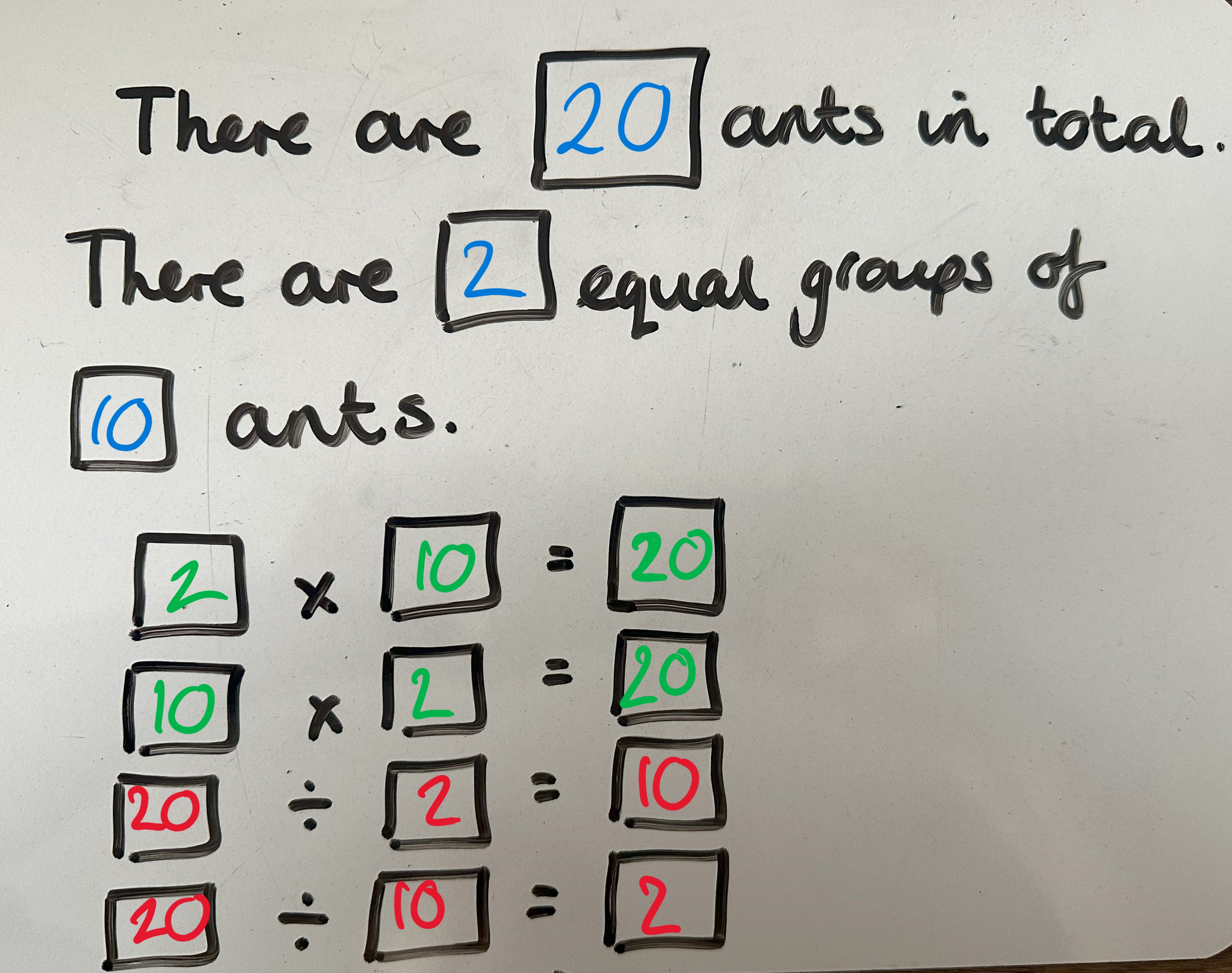

Teaching ideas for KS2 classrooms
Exploring arrays and linking multiplication and division
Read the beginning of the story to set the scene and stop after the ants arrange themselves into 2 lines of 50. As discussed previously, this can then be modelled using a 100 bead beadstring.
Children could then be tasked with finding alternative formations the ants could march in.
- Can children create their formations/arrays using beadstrings?
- Can they find all possible formations the ants could march in?
- Can they predict which order the formations will appear in the story? Why do they think this might be?
- Using the speaking frame mentioned previously, can children list all of the multiplication and division facts for their formations? What is the same and what is different about 2 lines/groups of 50 ants and 50 lines/groups of 2 ants?
Read the children the rest of the story. Do their formations appear? Would the ants be quicker marching in 2 lines of 50 or 50 lines of 2?
Solve a related multiplication and division problem
- Use the story as a stimulus but change the number of ants marching to the picnic and explore the possible formations.
- Compare the number of formations possible for different numbers of ants by exploring the validity of a theory, such as:
There are 2 groups of ants.
One group is made up of 30 ants and one group is made up of 35 ants.
Because 35 is a larger number, I think that means the ants could march in a greater number of formations.
Exploring factors
This story also acts as a great stimulus for exploring factor pairs of a number. And instead of factor bugs or beetles, why not draw factor ants!
Here are my efforts of drawing and completing a factor ant inspired by the illustrations in the book!

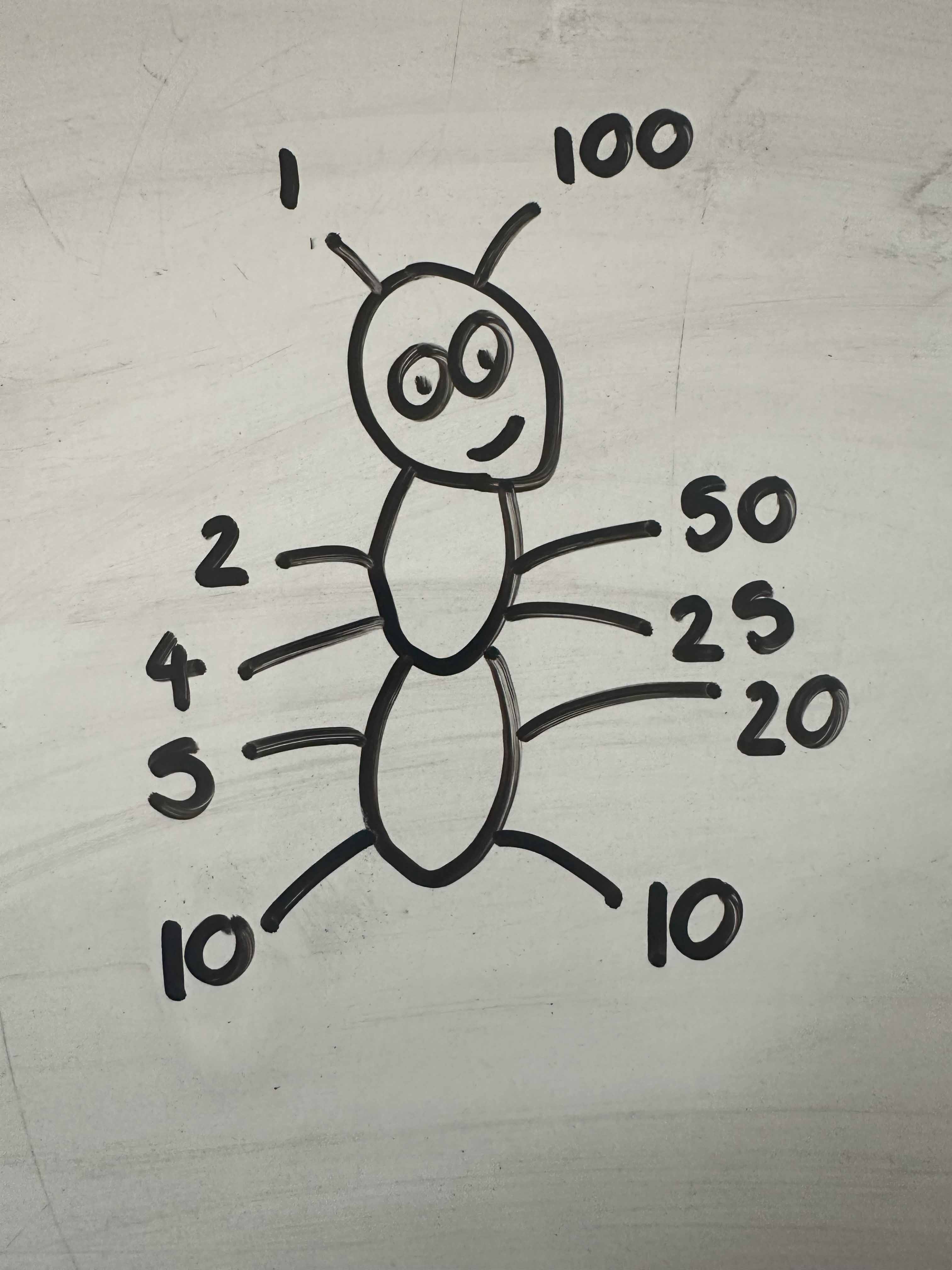
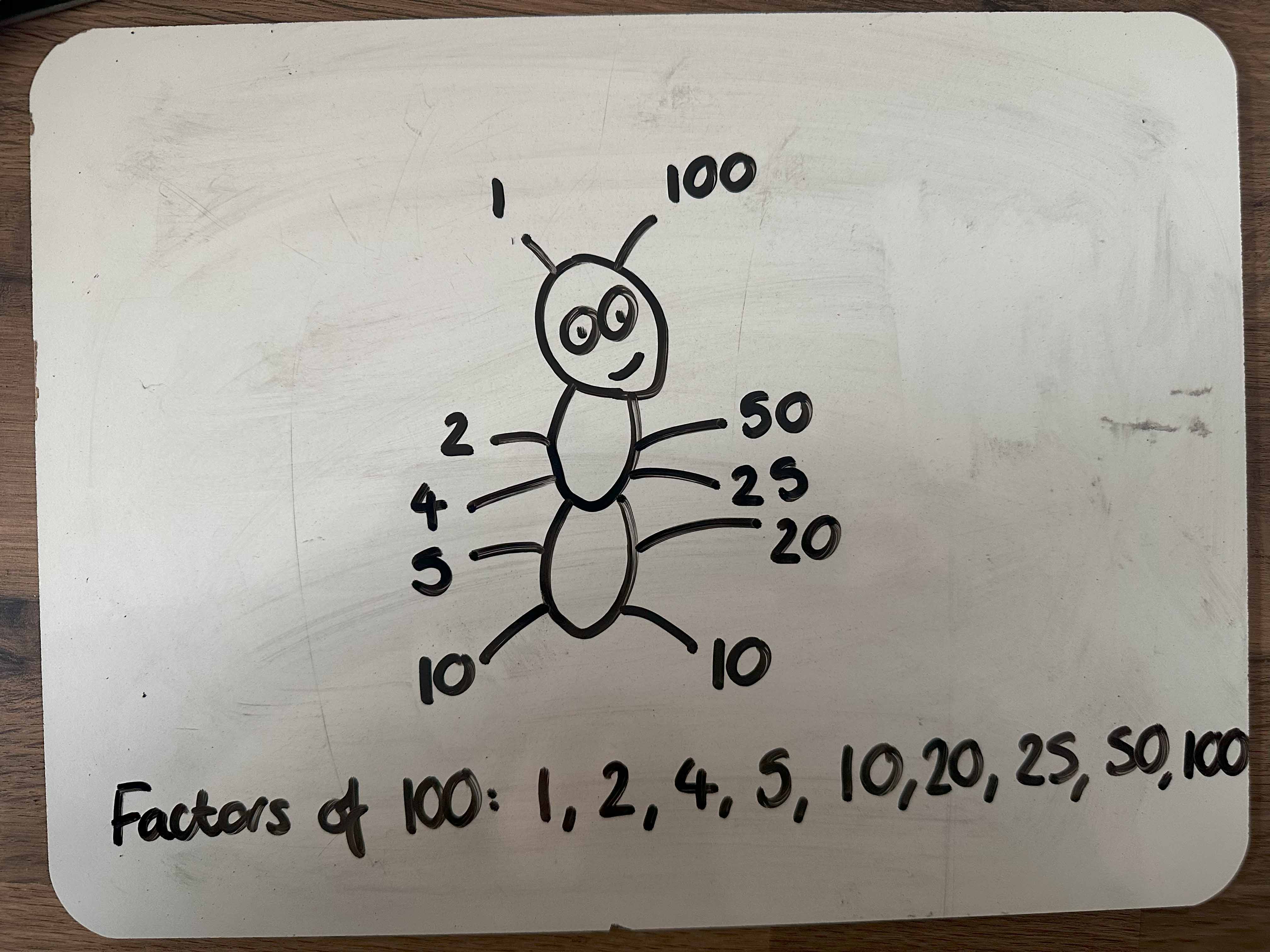
I appreciate that these ants won’t necessarily have the ‘standard’ six legs.
As above, the number of ants could be adapted and the number of total formations listed alongside the factors, making links back to commutativity; considering what is the same and what is different. For example, 4 x 25 and 25 x 4 – the same numbers are involved but the formations for these would look different!
As always, we love to see work children produce so please do email the team at primarymaths@hfleducation.org to share any examples that this blog may inspire!
If you have been inspired by ‘One Hundred Hungry Ants’, you may also enjoy, ‘A Remainder of One’, by Elinor J Pinczes. It tells the story of a bug called Joe who is part of the 25th squadron but always finds himself without a partner or group during parades. Poor Joe!

Spoiler alert! There is a happy ending for Joe!



