
One of the most enduring HFL Primary Maths blogs, which I continue to recommend almost six years after publication, is Siobhan King’s ‘Year 1 can’t record, can they?’
Having had the pleasure and privilege of diving into lots of Key Stage 1 (KS1) books this term, this new blog continues the sharing of great ‘real’ examples and experiences of teachers on their quest for effective and manageable self-recording for KS1 children.
Developing recording alongside concrete resources
First and foremost, the teaching and learning of maths should involve hands-on manipulation, be centred around high quality talk and be grounded in real life experiences.
Our first example is from October where Year 1 children at Mary Exton Primary School had been exploring flexible regrouping.
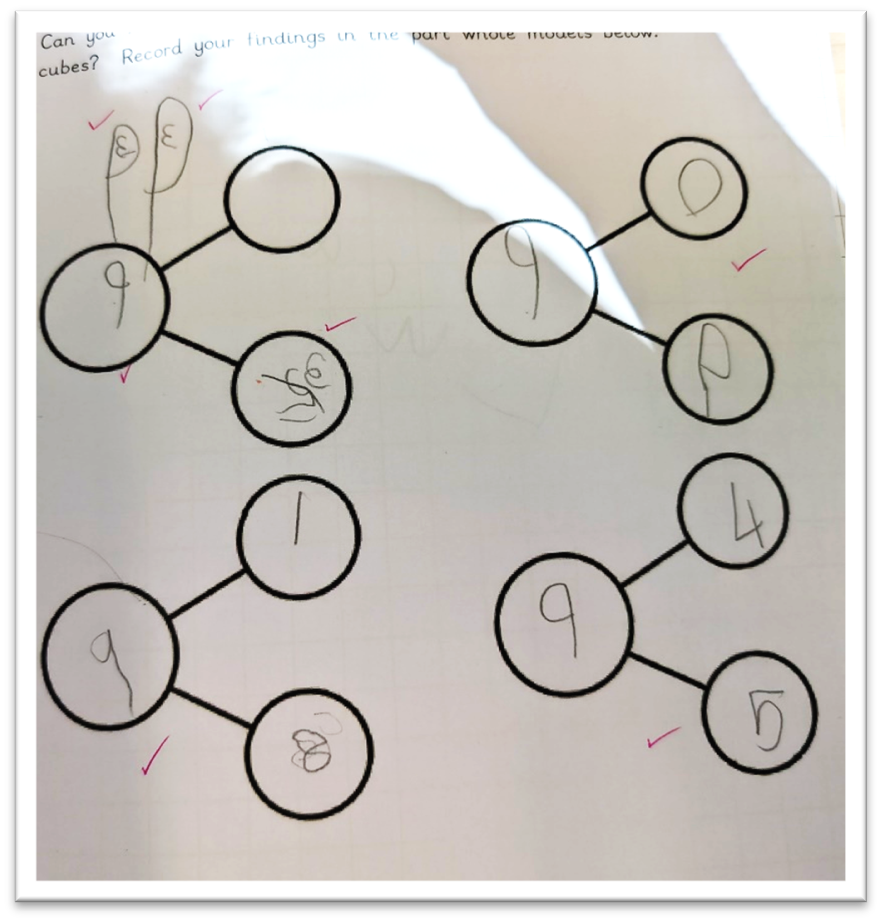
Children used nine cubes and a large, blank, part-whole model to explore regrouping the whole into different parts.
This recording frame was provided alongside the cubes and larger model to support children to record each regroup they found.
Whilst some pupils may be ready to translate directly from physical models to recording in the abstract with numbers, others may benefit from making the initial connection by drawing objects in part-whole models.
The development of pictorial representation has previously been explored by Gill Shearsby-Fox, who asked, “What do we mean by ‘pictorial’ in the CPA approach?”
Taking the plunge and opening up opportunities
One of my favourite moments of this academic year so far was when a teacher who had been tasked with increasing opportunities for Year 1 children to regularly self-record their maths, exclaimed, “I’ve taken the plunge!”
Progress in books was evident and pupil (and teacher) confidence had grown.
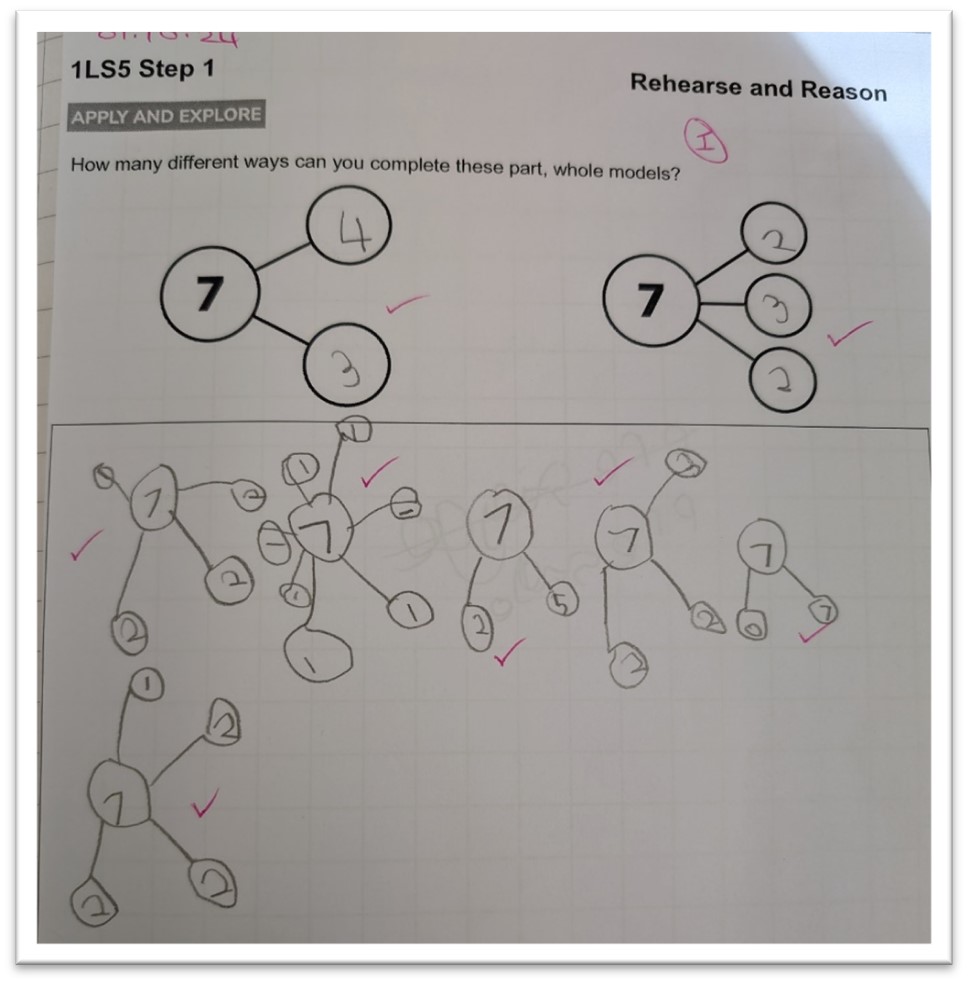
Here, the teacher had selected this question from the ESSENTIALMATHS Rehearsal and Reasoning sheets as a scaffold for recording alongside practical exploration with concrete resources.
The two pre-drawn part-whole models got the children started and provided an example of how they could record their thinking.
Blank space gave children the opportunity to demonstrate understanding of the concept independently, outside of the scaffold provided.
In this case, the child was able to use the original structure and take it a step further, beyond three parts.
Number formation
One thing I’m often asked is, “Does it matter about the formation of the numerals?” I would say yes… and no.
In the same way we wouldn’t want to critique the handwriting of every piece of English writing, overfocusing on numeral formation can distract from the mathematical focus of the learning.
Do we want to model correct formation, provide aids for the pupil to refer to and see an improvement over time? Yes!
A quick prompt or reminder may be enough for some pupils. Others may need support and intervention at a separate time to work on number formation and/or fine motor skills, as some children do with handwriting.
Model, model, model
The principles of effective modelled writing used in English lessons can also be put to great use in maths whereby adults voice their thoughts and model the choices made as they put pen to paper.
In my previous classes, we talked about ‘brain paper’. I would try to show the children what was ‘in my brain’ and how I was going to use the paper to support my thinking and calculations.
Large-scale modelling on the whiteboard or on flipchart paper creates a worked example that’s clear for all pupils to see.
However, one child taught me a valuable lesson. When I asked why his drawings of base-10 equipment spanned the whole A4 page, he replied (quite rightly) that, “They are the same size as your ones”.
To translate between large-scale whole class models and appropriately sized representation for children in their books, a visualiser is a great tool.
Having your own maths book with the same layout as theirs and recording in it ‘live’ under the visualiser provides the opportunity to explicitly demonstrate your thinking, e.g., “Oh dear! I’ve drawn it so small I can’t use it to help me!” This can pre-empt common issues before they arise.
Fading recording scaffolds
Do you have children in your class who can complete tasks with a scaffold but struggle when it is removed?
This is where gradual fading comes in.
A useful metaphor is that of scaffolding around a building being removed gradually once it has served its purpose and the structure can stand on its own.
This fading scaffold used with a Year 2 class, exemplifies how to quickly shift children from supported to independent recording in carefully designed small steps.
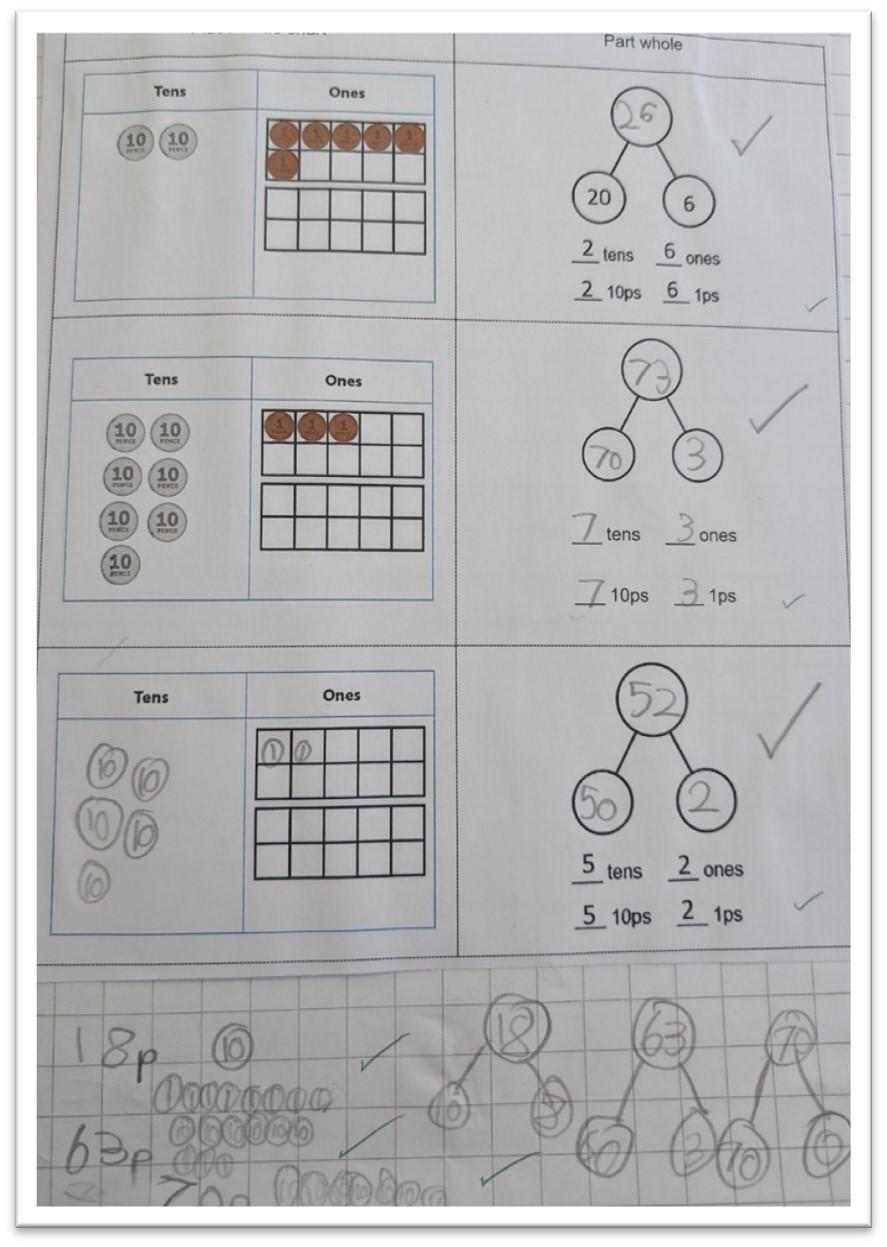
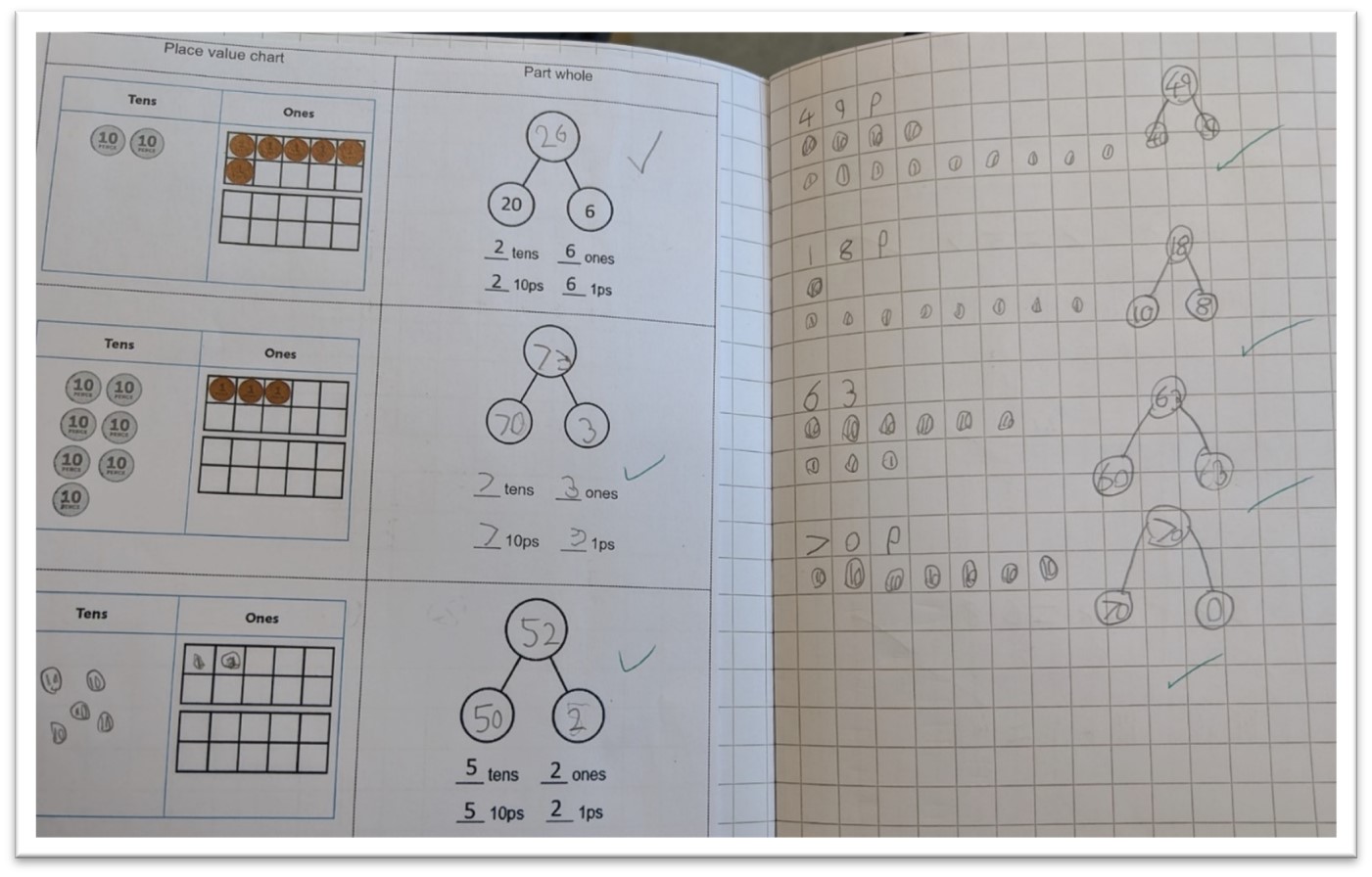
First, the pictorial model of coins in the place value chart is provided so children can use it to complete a part-whole model. By the third example, the template is provided but children need to draw the tens and ones. Crucially, children are then given time and space to create their own examples.
When providing scaffolded rehearsal, it is important to consider when children may need a faster or slower fade. Some pupils may move onto independent practice sooner and some may benefit from completing further scaffolded examples at each stage.
Recording gaming
“We did a practical activity / played a game, but nothing went in the books, so it looks like we didn’t do anything”.
This is something I hear fairly frequently from teachers and leaders.
As a maths team, we value and promote the idea of children making jottings while playing games and during other practical activities, but not necessarily for the purpose of providing “proof” that it took place.
As well as giving the activity more status, it is also a great opportunity for formative assessment. Looking at children’s notes allows teachers to identify what children have understood and taken from a game, as well as highlighting any errors or misconceptions that might be difficult to keep up with during the gaming itself.

Through recording, pupils are re-engaged in thinking. They need to identify what they consider significant, and therefore important, about the game.
The act of reflection allows them to filter what they need to keep and what they can throw away, enhancing long-term, meaningful memories.
Also, it allows the teacher to see what the pupils are identifying as the key learning points from the game.
Gaming Index Guidance, ESSENTIALMATHS
Recording reasoning
It can feel challenging to get children in the early stages of learning to read and write to respond to mathematical questions.

These Year 2 children have responded in slightly different ways to the same destination question, each demonstrating their understanding of the concept.

Responses to questions don’t have to be in the form of written sentences. Drawings, labels, jottings and verbal responses scribed by an adult all allow children to articulate their thinking.
Exposing the structure of concepts
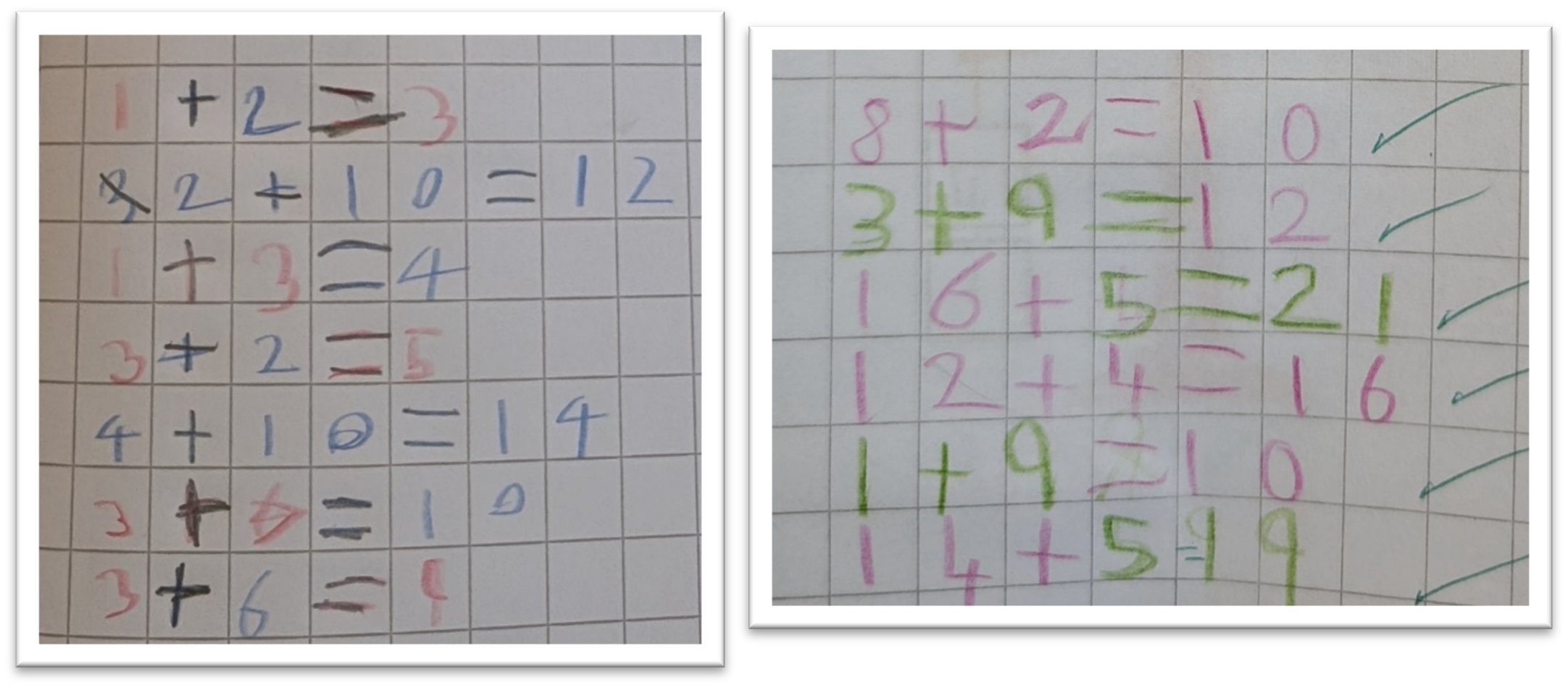
In the Year 2 books at Stonehill Primary in Letchworth, I was struck by the visual effect of colours used in different tasks to support children to spot patterns and notice connections.

Here, the use of the coloured pencils supported pupils to see how the value of two-digit numbers is represented with tens and ones, so that ‘twenty-six’ is recorded as ‘26’ not ‘206’.

The examples below show coloured pencils being used to explore the result of adding odd and even numbers. Visually highlighting patterns in this way can support pupils on their journey to making generalisations.
Demonstrating depth of understanding

This Year 2 teacher has chosen to provide children with a modelled example of talk. This pupil has taken this example and translated it into one of their own, representing their thinking pictorially and in the abstract.
A scaffold could have been provided here but this child, given the time and space, has not only demonstrated understanding of the vocabulary used, but has also made a crucial, and independent, link to calculation.
Recording as a window into a child’s mathematical mind
The value in recording in maths books is truly seen when there’s a shift from…
“We need to get something in the books to prove we did X.”
to
“Working on self-recording allows pupils to benefit from demonstrating their understanding and helps me to pinpoint misconceptions. It informs what I teach next.”
Where recording is celebrated and seen as an invaluable tool by staff and pupils to aid and support teaching and learning, it is no longer seen a chore, or something to squeeze in at the end of the week to ‘tick a box’.
Is recording in KS1 a walk in the park? Not always! But it can provide a fascinating and useful window into a child’s mathematical mind and what they may need next.
Are you looking to enhance the way your primary school pupils learn and engage with mathematics? Our dedicated primary maths teaching and learning advisory team is here for you.



