What do we mean by ‘pictorial’ in the CPA approach?

Do we encourage young children to draw pictures when engaging with the CPA approach? Are these pictures important?

I am a great believer in the importance of using Bruner’s Concrete, Pictorial, Abstract approach to support the conceptual development of mathematics with pupils of all ages. 

With our younger pupils, it is also important that the children get time to explore and play with a wide range of resources. 

But do we give young children enough time, space and encouragement to develop the pictorial aspect of CPA and is this necessary?

My short answers are no and yes.

No, I don’t feel we encourage or appreciate the importance of pictures in mathematics and yes, this is necessary.

Like all areas of development, children’s mark making is an essential skill that we must learn because mark making can be refined and developed into writing and drawing, both of which are a way of recording our explorations, thoughts, and interpretations about the world around us.

The new statutory Early Years framework for mathematics doesn’t explicitly mention mark making or recording. It does however state that:

“By providing frequent and varied opportunities to build and apply this understanding, children will develop a secure base of knowledge and vocabulary from which mastery of mathematics is built.”

I would argue that varied opportunities need to include opportunities for children to record their thoughts and reasoning through mark making. In both the Birth to 5 Matters and Development Matters they make explicit reference to mark making:

• experiment with their own symbols and marks as well as numerals.
  (Development Matters, page 89)

• discuss the different ways children might record quantities (for example, scores in games), such as tallies, dots and using numeral cards.
  (Development Matters, page 94)

• explores using a range of their own marks and signs to which they ascribe mathematical meanings.

• value and support children to use own graphics when problem solving
  (Birth to 5 Matters Range 5, page 99)

• begins to explore and work out mathematical problems, using signs and strategies of their own choice, including (when appropriate) standard numerals, tallies and “+” or “-“

• talk to children about the marks and signs they use to represent and communicate their thinking. As appropriate, model and discuss informal and standard ways (e.g. using arrows, plus and minus signs).
  (Birth to 5 Matters Range 6, page 102)

I feel this is a positive move as the focus on the numeral does seem to have decreased, especially in the Birth to 5 Matters document. I am not saying that the numerals aren’t important; they are, but they are a highly abstract representation of value, and it is the values they represent that we need young children to master. Linking illustrations of the values eventually to the numerals, will help to ensure that children know the ‘three-ness’ of three, for example. 

Statements from Range 6 that encourage mark making that exposes mathematical thinking, I am especially pleased to see. It is the talk that accompanies the marks children make that can give a true insight into their mathematical thinking and depth of understanding. As Worthington and Carruthers (2003, pg 83) say:

“When adults really listen and observe the marks children make, they will see beyond the scribbles and understand the child’s intended meaning.”

We need to provide opportunities and encouragement to enable mark making in a way that is open to the child and ensure it is given the reverence it deserves.

Let’s look at some examples of children’s drawing of two:

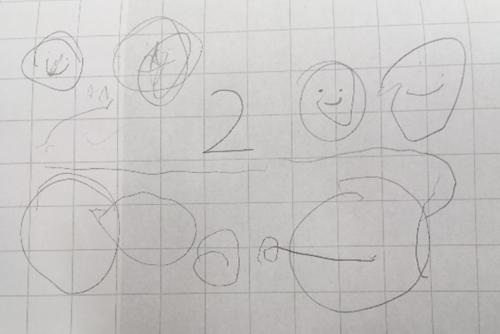
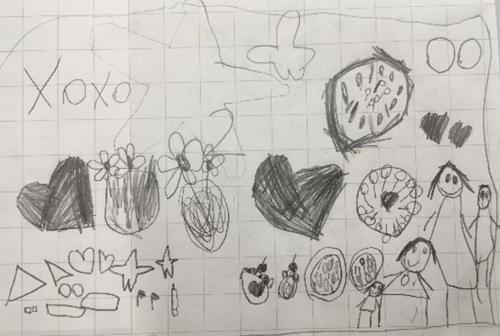
Before completing these pictures, the children had been exploring ‘two’ – observing pairs of objects in their environment and subitising two. All the children have presented two (the digit was written by the teacher) and all demonstrated a good understanding.

Initially, from the pictures, you could argue that the drawings in Fig. 1 don’t clearly show two but from the conversation with the child, they explained their collections. The two ‘faces’ in the top right are their mum and dad; dad has a beard – the additional marks. The other two faces were the child and their brother.

The picture underneath the family (that initially looks like five circles) is actually the side view of their favourite car. The child explained that they knew cars had four wheels but when viewed from the side, you only saw two – half of the wheels; that’s why it was a side view of the car.

The child who completed the collections in Fig. 2 was very methodical and even though some of the pairs of objects look very similar, they explained each set.

Finally, in Fig. 3, this child’s drawing is probably the most realistic but again, it is the conversation we had that demonstrated to me that this child’s understanding of two was deeper than the others because they demonstrated that you could have units of two that could be repeated – this is the start of understanding multiplication – but it was the most basic of their drawings that demonstrated this understanding.

When I asked the child to explain the ‘two’ in the XOXO part of their drawing, they told me that it was a pattern and there were two bits in the pattern (XO) that were then repeated. They went on to explain they had done that with the flowers as well; two flowers in each of the two vases.

From looking at the pictures, without talking to the children, I would have probably said that the child who draw the pictures in Fig. 3 knew the most about two, and the child who draw the pictures in Fig. 1 knew the least. This might be true but from the conversations with the children, the child who drew the side view of the car not only demonstrated their understanding of the value two but also indicated that they understood half.

For me, this example highlights several points:

• opportunities to have less structured and pictorial recording occasions are important
• when children are recording, take the time to talk to them about what they are representing
• don’t be influenced by the level of development of the mark making

Less structured recording opportunities

Many recorded maths opportunities rely heavily on worksheets; blank paper is available, but work done on this is rarely kept or valued. From questionnaires completed as part of the research carried out by Worthington and Carruthers (2003), only 16% of teachers referred to children making their own mathematical marks and recordings in maths lessons and in child-initiated play, and in another article by Worthington and Carruthers (2005), they say:

“without opportunities to explore their own mathematical thinking in their own ways and through their own choices of visual representation, children are prevented from developing their own understanding of the written symbols of mathematics.” (pg 5)

So how do we ensure opportunities for pupils to create their own marks and jottings and incorporate the practical resources and ensure that pupil’s maths books are presentable and that they help show the children’s progression through the learning?

Let’s consider the use of concrete resources to support maths learning.

I would never suggest not using a range of practical resources, but we have to ensure that pupils don’t become over-reliant on them or use them purely procedurally and therefore don’t make the link between the actions they carry out with the resources and the abstract calculations they are completing.

Clements and Sarama (2014) say that children must be moved along the learning trajectory and if they are reliant on manipulatives to do arithmetic in grade 2, they will continue to be reliant in grade 4 (page 319).

In the summary of Chapter 3 of the EEF guidance report: Improving mathematics in early years and key stage 1 about manipulatives and representations to develop understanding, it recommends:

That children understand the links between the manipulatives and the mathematical ideas they represent

I am seeing more and more children knowing what the resources represent, for example a base-10 rod is a ten, but they don’t know how it can be used and manipulated to support calculation.

There is a clear rationale for using particular resources to teach a specific concept

Pupils and teachers aren’t always clear about how or why a resource is helpful to support learning a concept and the use of resources become part of a process and don’t help to develop conceptual understanding.

Encourage children to represent problems their own way

This links back to what we have been talking about. Often, pupil’s books that I see do have mathematical representations in and some pupils I speak to can explain the model (i.e. the process of creating it) but they don’t necessarily understand what it is representing.

I encourage teachers to provide opportunities for pupils to represent their thinking in their own ways, ensuring that those marks / drawings / representations are given the same gravitas as all other recordings. I would also encourage them to be permanent. What I mean by this is not on a white board or a scrap piece of paper. If they have permanence, they have importance.

I appreciate that doing this is difficult, both in the early years and in KS1. There is a fine balance between keeping everything and handling recordings in a way that are manageable and purposeful, especially as expectations increase for recording working within KS1.

I sadly don’t have a definitive answer about how to do this (Siobhan King has some great suggestions in her blog, Year 1 can’t record, can they?) but I do believe that records of pupils’ mathematical activities need to illustrate learning or thinking, and often what is recorded doesn’t always show that and what does show this, the jottings and marks, are not kept and seen as unimportant.

I know as an upper KS2 teacher, the battles I had with pupils to get them to show their working and if they did do working, it was always on a white board or rubbed out. They didn’t see their jottings as important; if anything, they saw them as a failing because they weren’t always ‘proper’ maths in their eyes. Perhaps if we were to encourage and celebrate mathematical mark making more when children are younger, they would be more confident and prouder of their less-formal recordings when they are older. 

Developing understanding of pupils’ mark making

In the example described above, I have already highlighted the difference a conversation with the child can make to the adult’s understanding of the child’s mathematical thinking.

How can we understand pupil’s mark making better?

My first love is art, not mathematics, and I had the privilege of doing a joint degree in Primary Education and Art at Exeter University which included modules on art education and children’s drawing development. In my lecturers’ Linda Green and Robin Mitchell’s book (1997) – that I dug out of the loft – they summarise research into drawing development and describe stages of drawing as follows:

• scribbling stage (age 2 to 4 years) – random marks that can represent events and movements
• pre-schematic stage (ages 4 to 7 years) – emergence of repeated shapes which stand for something
• schematic stage (7 to 9 years) – schemas that describe form are developed
• Gang Stage (9 to 12 years) – drawing realism

At a similar time that children’s drawing development was being explained, Hughes (1986) was researching how 3–7-year-olds recorded quantities and the operations of addition and subtraction. He noticed that despite being taught numerals and operational symbols and equations when given a problem, children didn’t use these, and he classified the children’s responses under four headings:

1. idiosyncratic – responses didn’t seem related to the number of objects present
2. pictographic – representations related to the appearance of what was in front of them as well as the numerosity
3. iconic – representations showing 1:1 correspondence with the number of objects, unrelated to the appearance of the objects.
4. symbolic – using conventional symbols to represent each quantity.

Looking back at the drawings in Fig. 1, 2 and 3, the children are at different stages in their drawing development.

The child who drew Fig. 1 is entering the pre-schematic stage; the repeated shapes represent things with some recognisable features. The child who drew Fig. 2 is within the pre-schematic stage and the child who drew Fig. 3 is in the schematic stage. Using Hughe’s classifications, Fig. 1 and Fig. 3 would be classed as pictorial and arguably some of the marks within Fig. 2 would be classed as iconic – the pairs of dots that look similar represented different objects.

Let’s look at another example of a child’s recorded thinking and consider both the stages of drawing development and Hughe’s classifications.

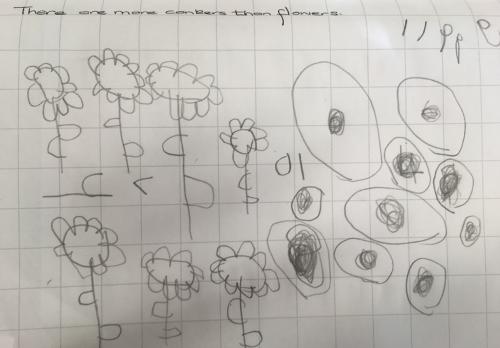
First, the stages of drawing…

This picture (Fig. 4) is clearly of flowers and conkers – repeated shapes have been used to create the images, so this child is moving from the pre-schematic stage to the schematic stage.

Now Hughe’s classifications…

It is pictographic – the child has drawn a picture of the flowers and conkers; they haven’t drawn symbols or images that represent the real objects. In addition to the pictures, I can also see some numerals; there is clearly 0 and 1 together and there are 10 conkers – this is an attempt to show the amount of conkers with numerals. There is another mark that could represent the number of flowers. So, this child is beginning to use symbolic marks as well.

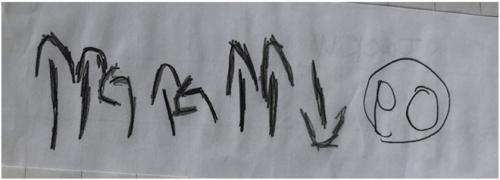
And finally, Fig. 5…

For this task, the children were asked to draw the instructions to programme a route for a Bee-bot to follow; arrows have been used to symbolise the instructions. This child has possibly taken cues for the symbols from the Bee-bot but the symbols they have used give clear guidance for the reader to follow. It would be symbolic using Hughe’s classification but thinking about drawing development, it is a simple drawing and arguably isn’t a picture. However, what it is communicating is clear.

Does the quality and accuracy of a child’s mark making correlate to their mathematical knowledge and understanding?

To be honest, looking at pictures using the drawing development stages and looking at them using Hughe’s classifications, you are looking at them through two completely different lenses. When looking at children’s drawings, how realistic the drawings are should not influence our expectations of the thinking behind what the marks are representing – we mustn’t have conscious or unconscious bias.

Just because the drawing is more developed, doesn’t necessarily mean the mathematical thinking and reasoning is more developed.

If we think about Hughe’s classification, if the marks are classified as symbolic, you could argue that the mathematical thinking and understanding is more complex because the person using the symbols to express values or operations knows and understands this complex shorthand.

We have numerals and symbols like 9, +, ÷, < to represent values, operations, and comparisons because it is quicker and easier. A large part of maths learning is about becoming efficient and working out the best way to solve a problem or calculate an equation. Lots of the teaching of maths is helping children to understand and use this shorthand but we must give children time and space to make the connections between the real objects / problems, and how they can be represented.

I would argue that a critical part of this complex cognitive process should include giving children the time and space to develop their own ways of representing the real objects / problem. It will most likely be inefficient, time consuming and possibly unclear but as I mentioned previously, Worthington and Carruthers (2005, page 5) say;

“Without opportunities to explore their own mathematical thinking in their own ways and through their own choices of visual representation, children are prevented from developing their own understanding of the written symbols of mathematics.”

Once children have had an opportunity to explore with their own visual representation, it is our job to help them develop those thoughts and representations to become more efficient and this will involve using numerals and symbols. However, we must make time and space for these opportunities and not over-scaffold children’s mathematical thinking with worksheets or prescribed representations, or else maths will become what ‘painting by numbers’ is to art. It might create a lovely picture but can be completed without thought or understanding and isn’t retained or remembered.

Let’s celebrate and make opportunity for children to represent their mathematical thinking as creatively and purposefully – for the child – as possible. Taking the time to talk about what their pictures represent to them and using that information to help us understand the child’s thinking, is so that we can move their learning on successfully. This will enable them to make that difficult progression through the concrete, celebrating the pictorial, to the abstract with meaning and understanding.

I hope you agree with me that the pictures are important.

References:

Clements, D and Sarama, J (2014) Learning and teaching early math: the learning trajectories approach, Routledge

Davenall, J., Dowker, A., Williams, H. J., Gripton, C., and Gifford, S. (2021) Developing mathematical graphic in the early years 

DfE (revised July 2021) Development Matters

DfE (updated Sept 2021) Early years foundation stage statutory framework

Early years coalition (2021) Birth to 5 matters www.birthto5matters.org.uk

Green, L. and Mitchell, R. (1997) Art 7-11 developing primary teaching skills, Routledge

Hughes, M. (1986) Children and Number: Difficulties in Learning Mathematics. Oxford: Blackwell

Worthington, M and Carruthers, E (2003) Children’s mathematics: making marks, making meaning, Paul Chapman publishing

Worthington, M and Carruthers, E (2005)The art of children’s mathematics: the power of visual representation (PDF) The Art of Children's Mathematics: the Power of Visual Representation (researchgate.net)