Inspire me! The CPA approach: using Cuisenaire Rods to reason with fractions SATs questions

In our previous blog, we explored how to secure understanding of the part whole relationship using Cuisenaire Rods. We focused on fractions and equal parts of the whole.

In this blog, I will model how Cuisenare Rods can be used to solve questions from KS1 and KS2 SATs papers. Building using the manipulative is a powerful tool in supporting children to develop their reasoning skills.

The problem with problems

As a team of maths teaching and learning advisers, we know from working in classrooms with teachers and children that solving worded problems is regularly identified as a priority area to develop across schools.

As Charley McKay explores in the blog If we keep testing in Year 6, they’ll just get it... right?, according to Polya’s four-step model (1957), learners progress through four stages when faced with a problem:

Often, it is in the first two stages where children make errors and misunderstand what the problem is asking of them.

This is where building through problems using Cuisenaire Rods can expose the mathematical structure, leading to realisation of the calculations required.

When modelling, a visualiser is a great tool to use to allow children to see how to build through a problem piece by piece. Talking through the problem as you go will allow them to make connections and then explore similar problems with a similar inner monologue. This may include making changes as things ‘don’t work’ for a particular problem, e.g., a rod choice needs to change.

When building through a guided example, children may benefit from some sentence starters to support them in sharing their thoughts and structuring their ideas.

I can see…
I think that…
I know that…
I have noticed…
If… then…

Let’s look at some previous SATs questions. Each has a slightly different structure to build through.

Key Stage 1 SATs questions: let’s build them!

Key Stage 2 SATs questions: let’s build them!

Let’s jump now to some end of KS2 questions. You will notice quite a shift in complexity, and we must bear in mind that children will acquire much new knowledge and many new skills between these two points.

Once children gain familiarity with the relative sizes of Cuisenaire Rods, they will be able to apply them with confidence to more complex problems, bringing in other mathematical domains.

The suggested sentence starters above still apply.

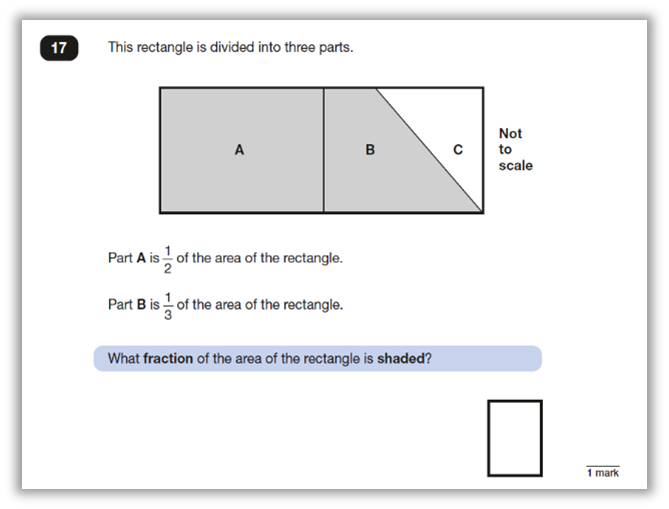
And now let’s look at how a fractions of quantity question was represented in this year’s paper. You may agree with me that this presentation was perhaps not as tricky as some that we have seen in previous years, but the structure is still very much worth exploring. 

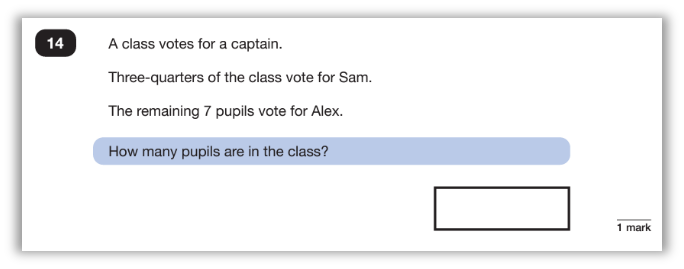
The connection between fractions and percentages can be revealed in a similar way.