
This is the first blog in our new series, ‘Inspire Me!’
In this series, we will take a manipulative and exemplify different mathematical concepts that you could explore using the concrete resource in your classroom.
The first resource that we will be focusing on is Cuisenaire Rods.

Not used Cuisenaire Rods before?
Have used them before and want to expand your repertoire?
Keen to challenge your confident learners through exploration of an alternative manipulative?
Invented in 1945 by a Belgian teacher, Georges Cuisenaire, there are 10 rods of different lengths and colours.
The smallest rod (the white rod) is 1cm in length and the longest rod (the orange rod) is 10cm in length. Other coloured rods measure between 2cm and 9cm.
Let them play!
We would suggest that when introducing your children to Cuisenaire Rods for the first time, you let the children ‘play’ and build with them.
Ask them to build a picture with them. Then give them some lines of enquiry.

If the white rod represents 1, what is the picture worth?
If the white rod is worth 2, what is the picture worth?
What if the white rod was worth 4?
Already we are exploring scaling and multiplicative relationships!
Cuisenaire Rods are a hugely versatile manipulative so let us inspire you!
Why use manipulatives?
Before I delve into how to use Cuisenaire Rods to explore the concept of algebra, let’s revisit the fundamentals for teaching concepts in mathematics.
In their ‘Improving Mathematics’ guidance reports, the EEF recognise that manipulatives and mathematical representations play an important role in developing mathematical understanding from Early Years to KS3 (1,2).
When selecting a manipulative, it’s important to ask yourself:
- How is this tool supporting conceptual understanding?
- Is this the most appropriate tool to scaffold learning?
- How will I enable students to work independently of the manipulatives over time?
Inspire me! Introduction to algebra
Fundamentally, algebra involves manipulating number to identify patterns and is described in the oxford dictionary as: “a type of mathematics in which letters and symbols are used to represent quantities”.
Children’s experience of algebra begins in the early years where they begin describing and noticing patterns. Pre-requisite understanding builds through part-whole exploration in key stage 1 and beyond.
Step 1: Play with the Cuisenaire!
With no numbers involved (yet), allow children time to revisit and secure their part-whole understanding before gradually making connections with the abstract form of expressions.
Provide children with a set of coloured rods and ask them to find combinations which are the same length as the brown rod.
For example:


When modelling the discovery of different combinations, share your internal monologue.
For example: “I know that two purple rods is equal to one brown rod. Purple + Purple = Brown.”
Provide children with time to explore other equalities with the rods using the following speaking frames to support them in making connections:



Step 2: make connections
Use the part-whole relationships the children have discovered between the colours to make visual connections with numeric values and represent ‘unknowns’ with letters.
Revisit complements to 10 or 100 with the rods. Give the whole a value.
For example:
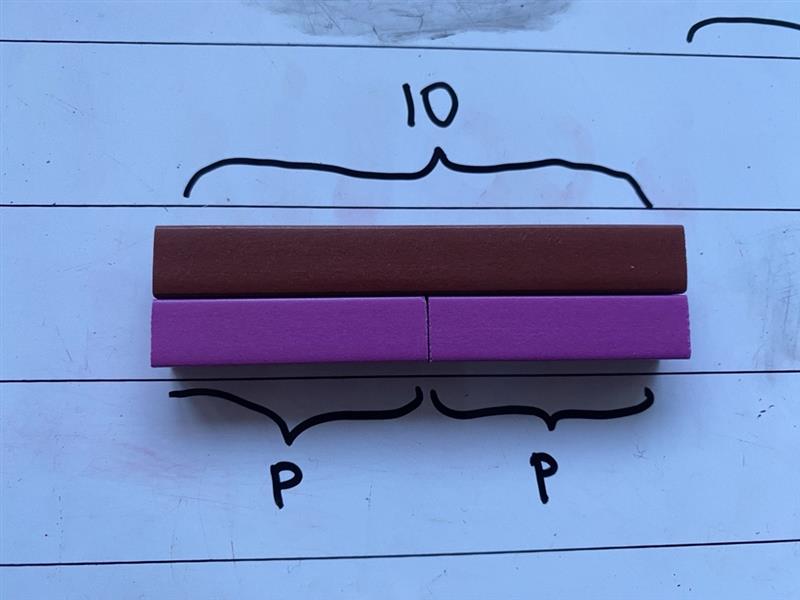
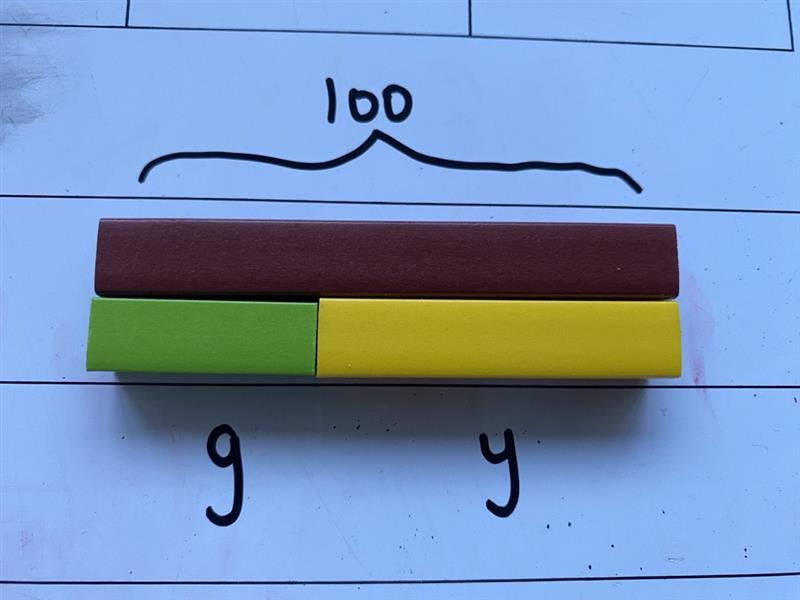
Model how to represent the ‘unknowns’ as letters rather than use their colour names.
p + p = 10 or 2p = 10
g + y = 100
The children can use the same, familiar speaking frame to support them to make connections.

At this stage, children are still exploring and looking at representing the unknown rather than finding it.
Step 3:
Once the children have grown confident and familiar with the Cuisenaire model, we can begin supporting them in making links to a familiar pictorial representation - the bar model.
For example:
Which bar models could be correct? Which could not?
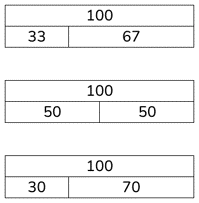
Extend the speaking frame from step 1:
Explore this further using expressions with an unknown, for example, x + 30 = 100
Step 4:
Provide children with an equation with one unknown.
For example:
x + 24 = 100
Children could represent this in a bar model.
Ask the children: If x + 24 = 100, what else do you know?
Explore creating a fact family with Cuisenaire Rods and bar models, labelling each part and the whole.
Application
Challenge children to apply what they know to a problem like the one below from the 2019 KS2 SATs paper 3 (reasoning):
Keep an eye out for more blogs from the Inspire Me! series this term. To subscribe to our blogs: Get our blogs straight to your inbox
Join the HFL Education Primary Maths Team for upcoming training and events
To keep up to date: Join our Primary Subject Leaders’ mailing list
References
1 – Improving Mathematics in the Early Years and Key Stage 1, https://educationendowmentfoundation.org.uk/education-evidence/guidance…
2 - Improving Mathematics in Key Stages 2 and 3
https://educationendowmentfoundation.org.uk/education-evidence/guidance…
3 - 2019 Key Stage 2 mathematics paper 3: reasoning
Contains material developed by the Standards and Testing Agency for 2019 national curriculum assessments and licensed under Open Government Licence v3.0.



