
Fractions – let’s go back to the start
Do the children in your class really understand what a fraction is? Is this holding them back when working with complex fraction concepts in upper key stage 2?
They may well be able to use terms such as ‘numerator and denominator’ to describe what a fraction looks like or how it is written but how secure is their definition of a fraction?
This is something that I have explored with several schools in recent weeks especially in Lower Key Stage 2 where children are finding problem solving with fractions tricky. So, in the words of Coldplay, ‘let’s go back to the start’, and explore the underlying structure of fractions. Cuisenaire Rods are a great resource to do this.
Using Cuisenaire Rods to explore
Often, pictorial bar models are used to explore the structure of fractions. I would encourage the use of Cuisenaire Rods first to then build up to using the pictorial representation alongside.
Recently, a Year 3 child who usually lacks confidence in maths gave me a super definition to describe a fraction: ‘a fraction is an equal part of a whole’.
I don’t think that we can argue with that!
What lead to this was exploration using Cuisenaire Rods to create part whole models.
Let’s explore a learning sequence
Depending on which year group you teach, you may need to adapt the chosen fractions used. For example, with Year 1 children, you may focus on models that expose halves and quarters.
Start with the whole and find the parts:

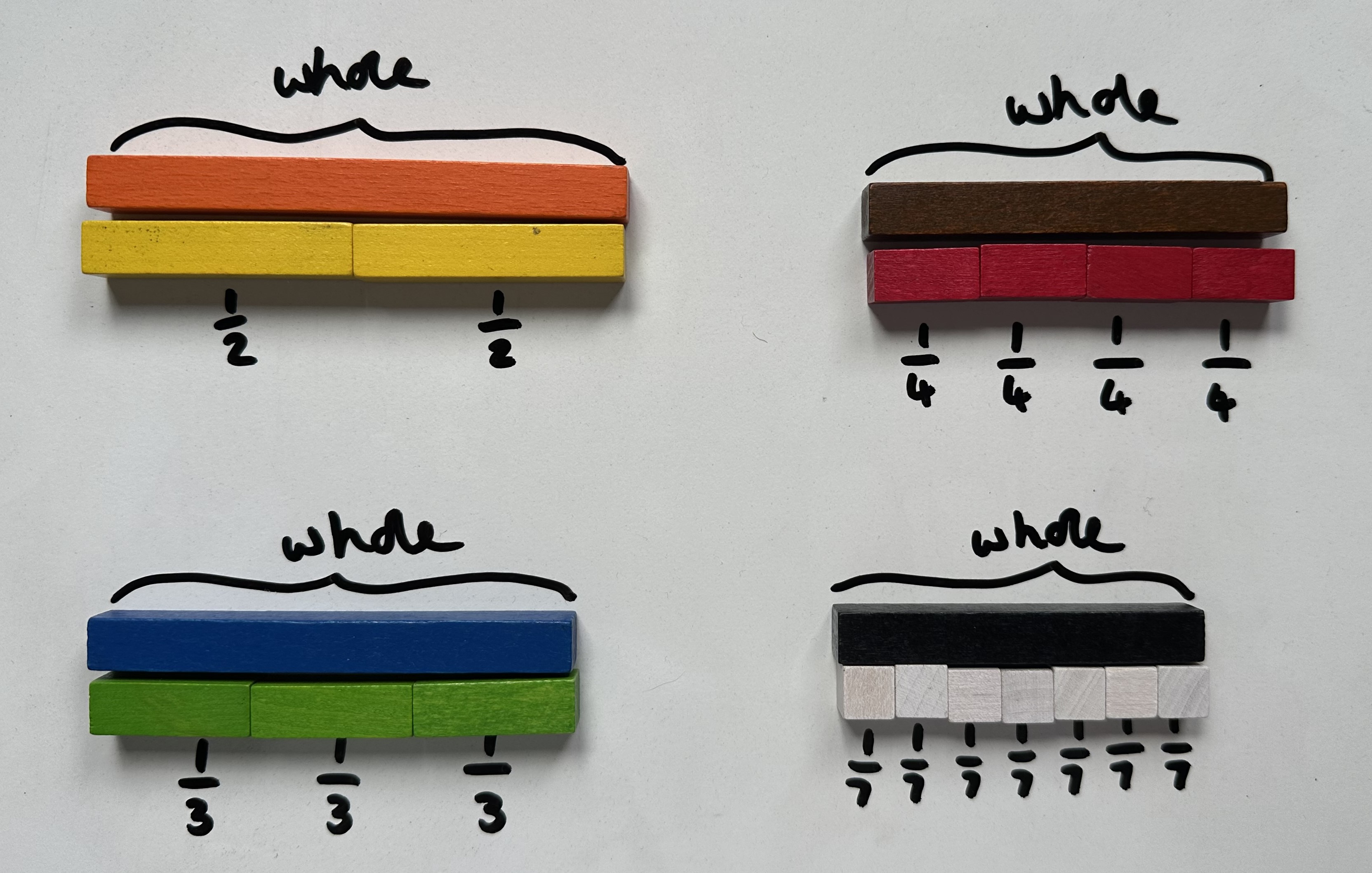
Labelling the whole will help to reinforce the relationship to part and whole models. You may choose to avoid labelling the whole as 1 or the numerical value of the rod (for example labelling the orange rod as 10)
The focus is understanding what a fraction is as opposed to finding fractions of an amount which could act as a distraction.
The parts could be labelled using the word ‘part’ or the fraction notation. Using the fraction notation will help to support the understanding of how many parts make up the whole. Children might be encouraged to say things such as:

This is also a good opportunity to make the link with division.

Investigation
Cuisenaire Rods can also be used to investigate which fraction models can be created and which cannot.
For example, children could explore which rods can and cannot be split in half or into thirds using other Cuisenaire Rods, as exemplified in this Year 2 step from ESSENTIALMATHS:

Parts of (or the whole) speaking frame could be used to support children’s exploration and discussion.

This speaking frame could be adapted and used with other fractions such as fifths, sevenths and tenths in Lower Key Stage 2.
Give the parts and find the whole:
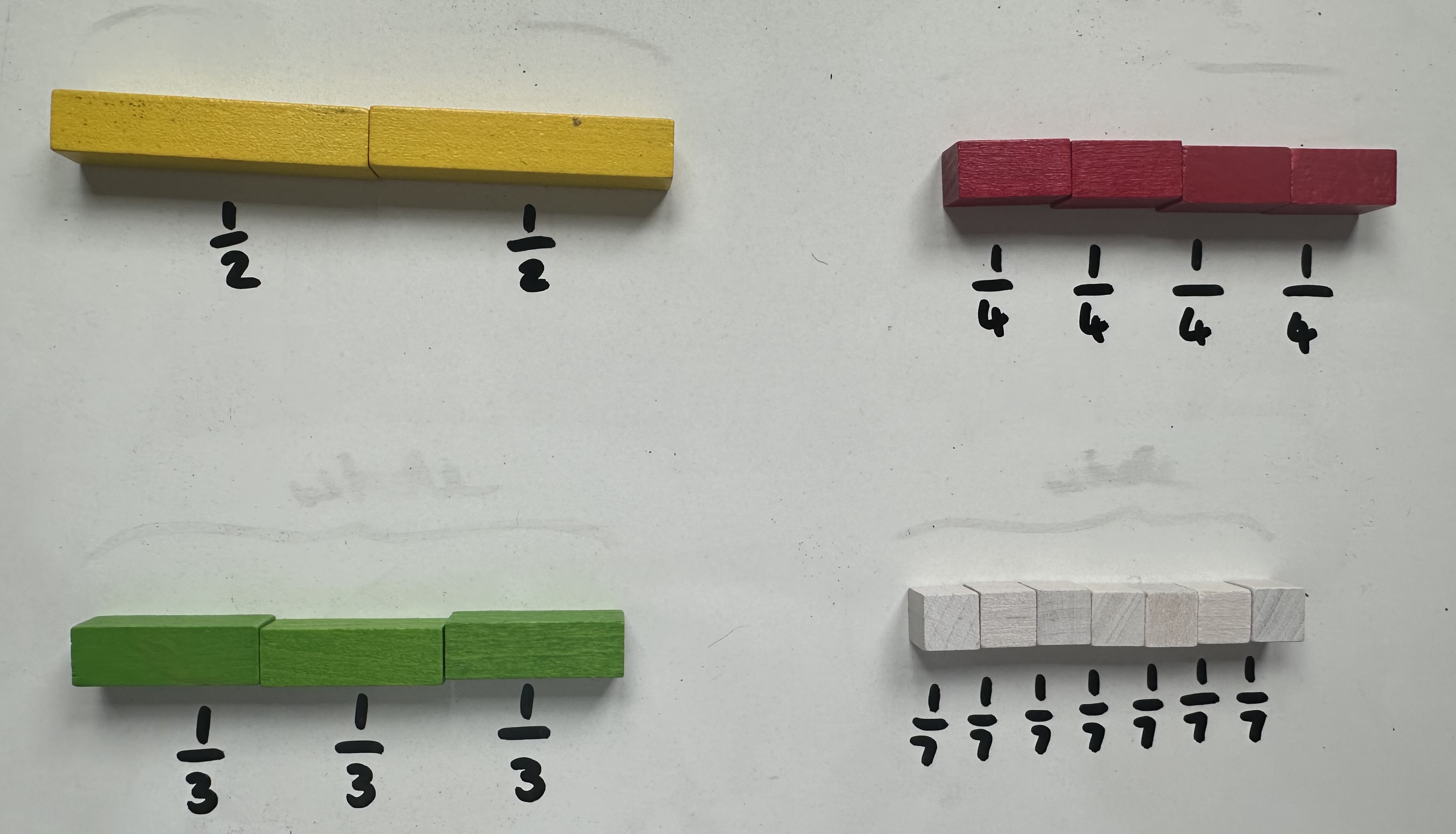
Provide children with the parts and ask them to find which coloured rod will represent the whole. For example, the orange rod would represent the whole in the example where the yellow rods each represent a half. Check that they understand that the whole must be equal to the combined parts.

To further clarify this, children could also create ‘non-examples’ to demonstrate their understanding of what a fraction is – an equal part of a whole.
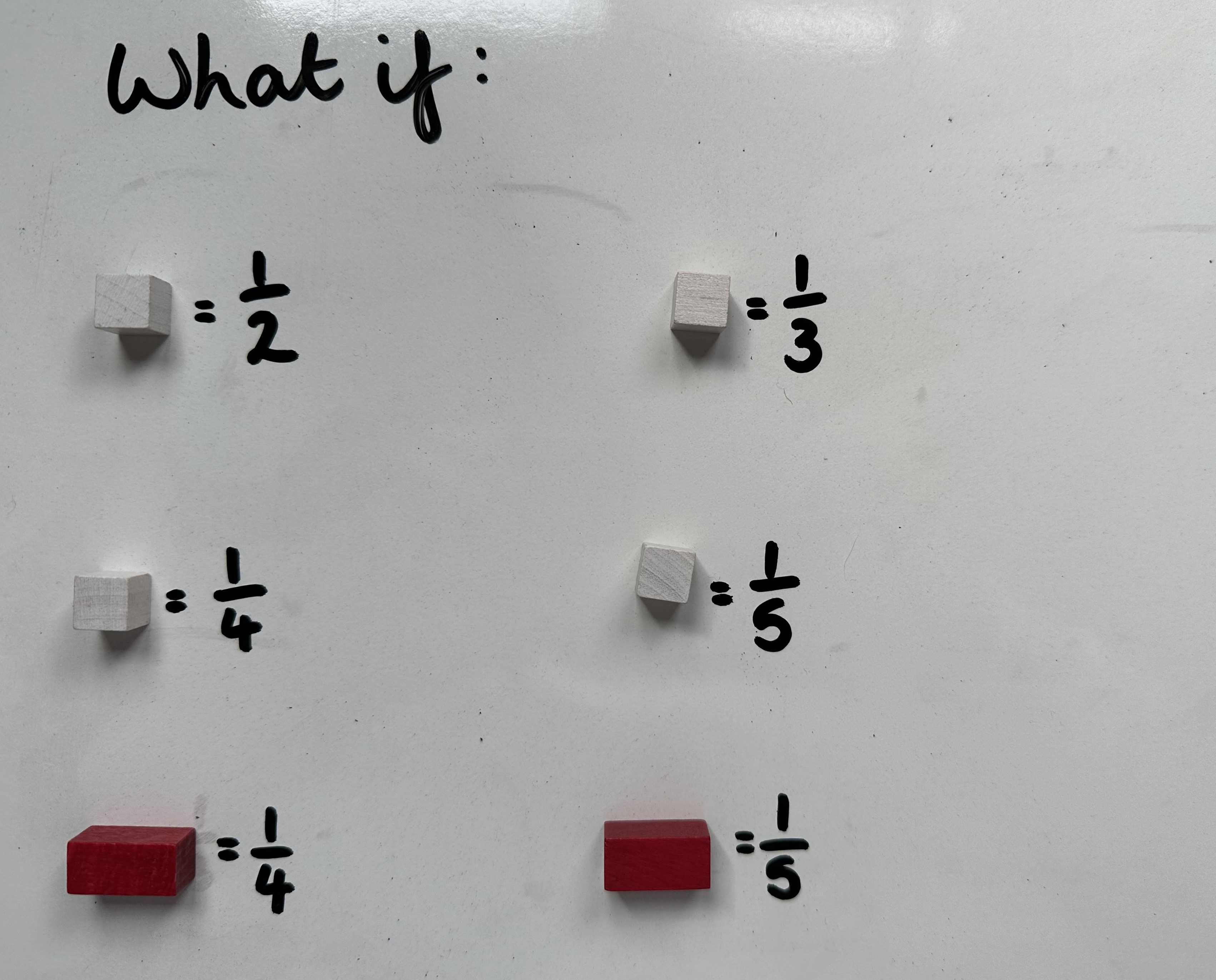
Can children build their own fraction models when a rod is presented as a unit fraction?
Do they understand that if the same colour rod (take the white rod in the first examples) is given a different unit fraction value, that the whole will also be different?
The fraction piece may be the same size, but the number of parts will dictate how big the whole is.
Rehearsal and reasoning through games – keep the learning fresh
Children will either need a feely bag full of Cuisenaire Rods or they could have some rods on a table covered with some paper.
Provide a description such as:
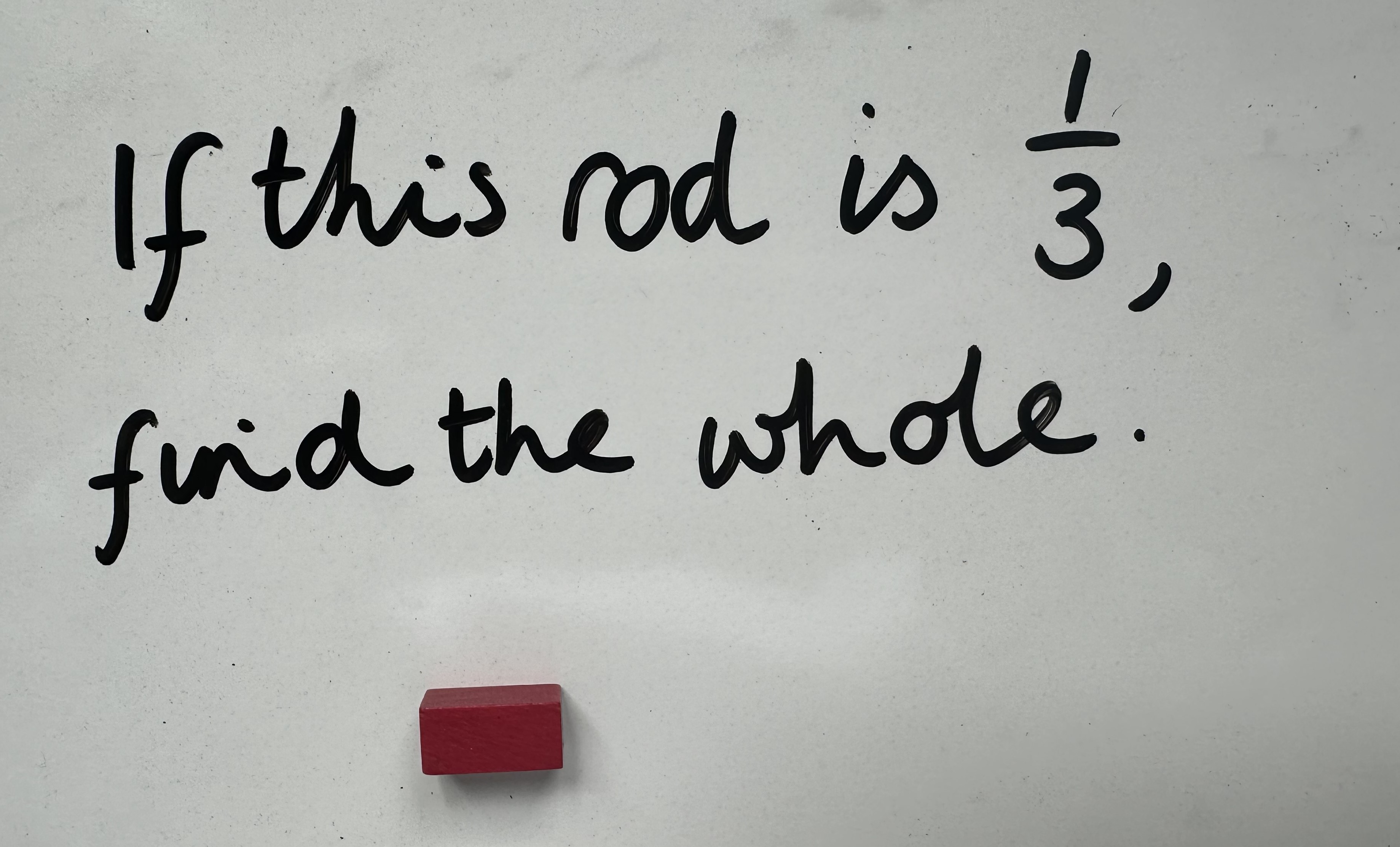
The children then need to use their estimating skills to feel for the rod which will represent the whole. Once they have found their chosen rod, the other rods are revealed so they can check whether they were correct.
This could be adapted to include decimals and percentages in UKS2. For example, if the purple rod is 25%, which rods would need to be joined to represent the whole (the orange and green rod in this case).
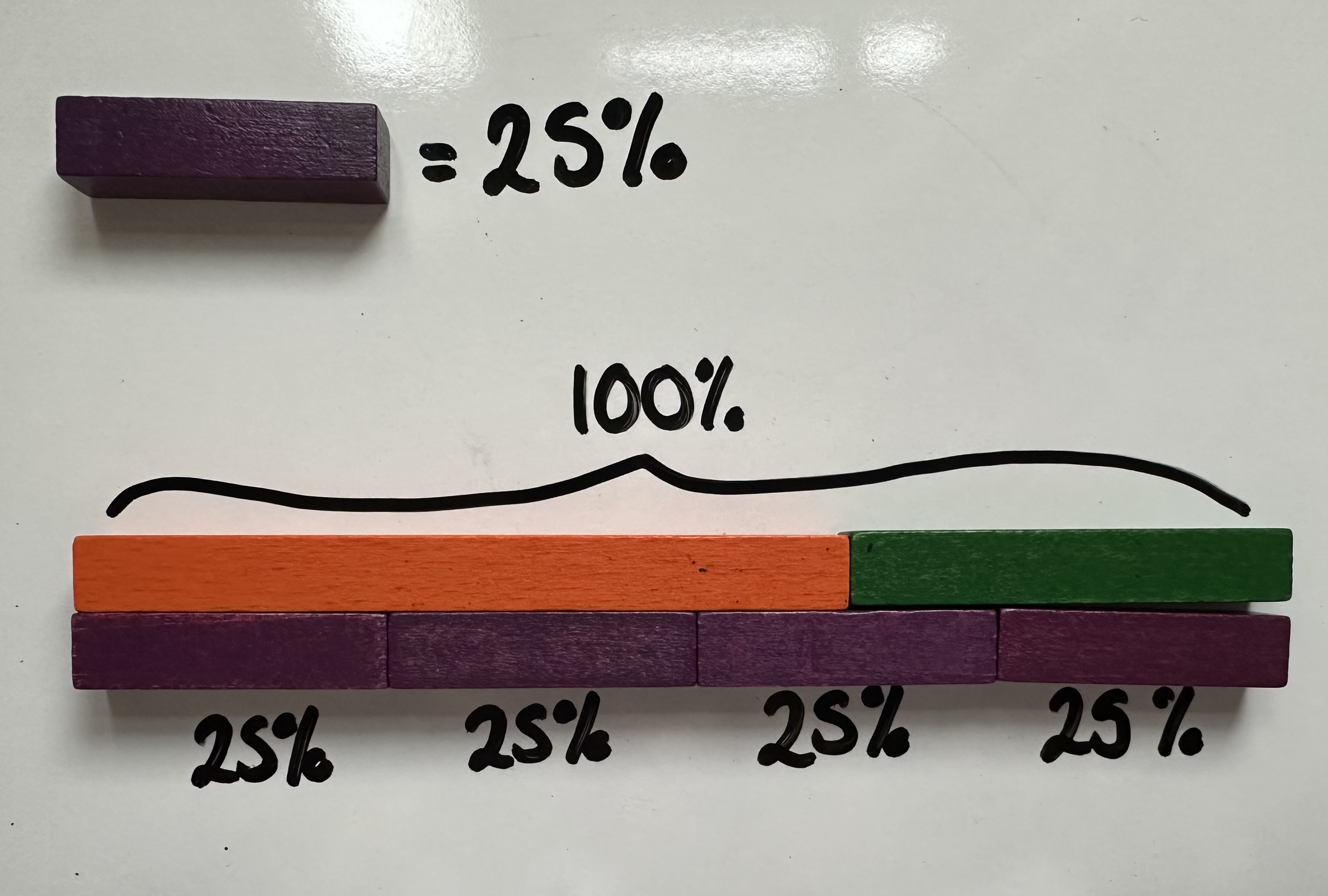
Building connections
Cuisenaire Rods are also a great way of introducing and exploring equivalent fractions.
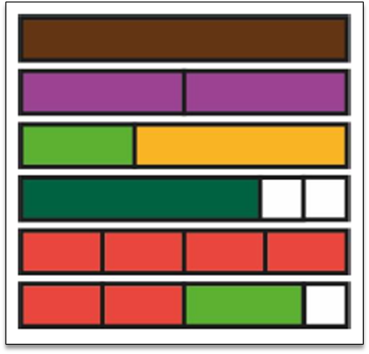
Children could start by building walls and looking for layers which are built from equal parts. They could also discuss which combinations of rods are not equal parts of the whole.
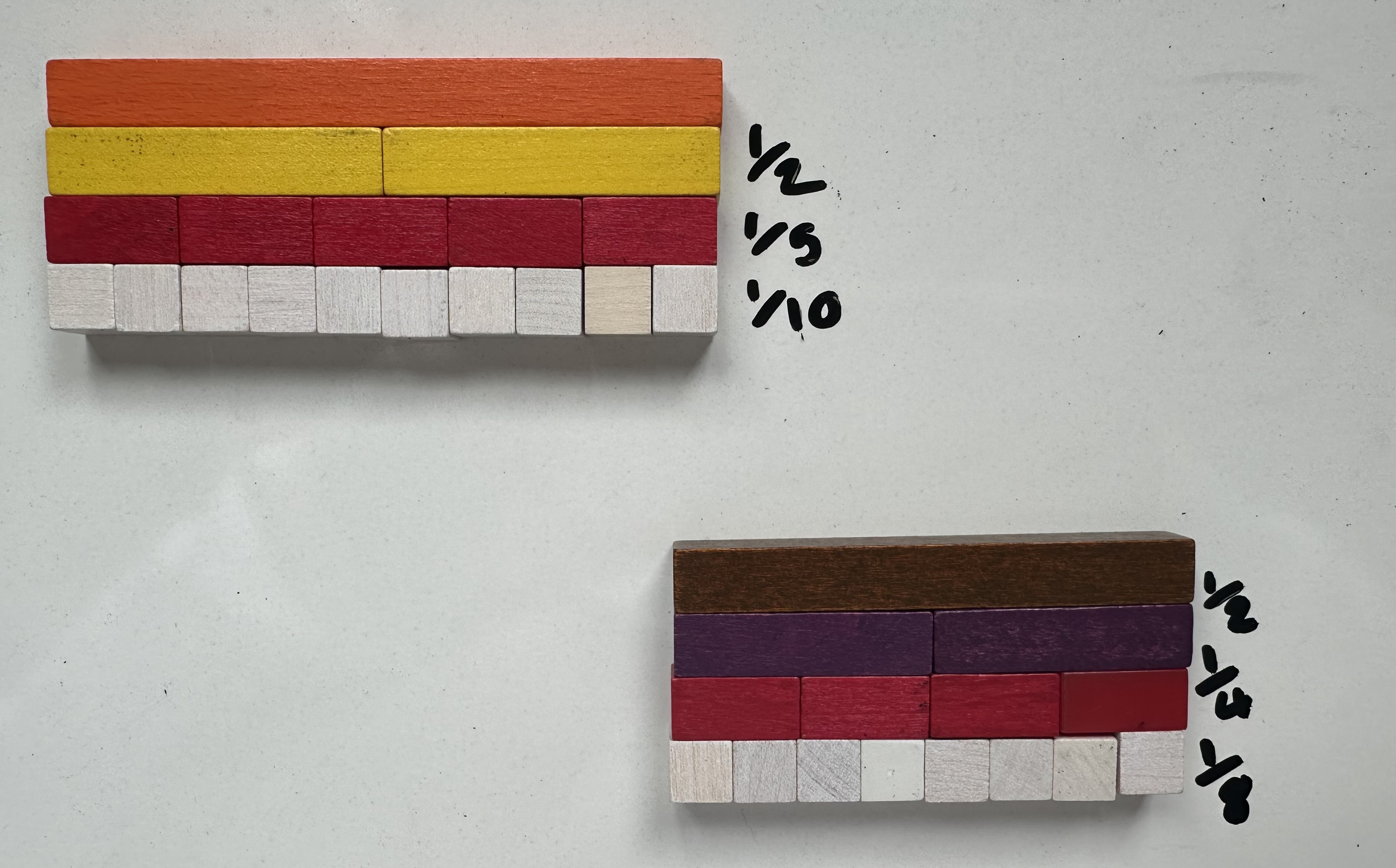
Children might add fraction notations to their models and then draw these pictorially.

These models also allow connections to be made and discussion had about factors and prime numbers. In these examples, the yellow and black rods represent 1. But what if the yellow rod represented 5 and the black rod represented 7? The yellow rod can only be split equally using other rods using 5 white rods. The black rod can only be split equally using other rods by using 7 white rods.



The rods could also be used to prove composite numbers.
This model proves that 9 is a composite number as it can be shown using ninths and thirds.
9 is divisible by 1, 9 and 3.
In our next ‘Inspire Me’ blog later this term, we will be continuing our focus on fractions and using Cuisenaire Rods to support problem solving involving fractions.
Other blogs in the ‘Inspire Me’ series focusing on Cuisenaire Rods:
Inspire me! Cuisenaire Rods: The CPA approach to teaching algebra
Inspire me! Using Cuisenaire Rods to explore calculation strategies



