
Regular conversations in schools
Through my work in schools recently, I have been having similar conversations regarding the effective use of manipulatives. Teachers and subject leaders tell me that they follow the CPA (concrete, pictorial and abstract) approach in the lessons for their year group but have admitted that although they may use a resource to teach an element of maths, they are not always aware of where that leads to in future years, or what has come before in terms of CPA.
For example, base 10 is used superficially to help reach an answer in formal addition, but the starting point of pupils building numbers, exploring number magnitude, regrouping ten ones into one ten and flexible regrouping may not have been considered.
In this way, CPA is used as a crutch rather than to develop deep conceptual understanding.
Clear intent and implementation
The guidance report, ‘Improving Mathematics in KS2 and KS3’, the Education Endowment Foundation (EEF) recommends teachers should ‘use manipulatives and representations’ and goes on to explain that ‘Teachers should ensure that there is a clear rationale for using a particular manipulative or representation to teach a specific mathematical concept.’
This sentiment is echoed in the equivalent EYFS and KS1 document ‘Improving Mathematics in the early years and KS1’. There needs to be a clear rationale for the choices made, both how and when, pupils move through the CPA process towards mastery of the concept.
Let’s track one concept through the CPA approach, across multiple year groups, and consider the choice of resource, and more importantly how and when it is used, so that it can deepen a child’s understanding as well as enable them to apply the knowledge in other ways.
We will explore the mental calculation strategy Equal Difference
Reception
It begins in EYFS where pupils begin to subitise small amounts (recognise how many there are without counting).
Using tens frames, pupils are encouraged to see numbers within numbers as they conceptually subitise the number 8 through seeing a group of 5 and a group of 3.
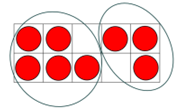
This leads to exploring the equals sign as a balance. At this point, pupils should be using the concrete resources and be beginning to explore a pictorial representation to allow them to internalise their understanding and ‘own’ it.
Year 1
Following that, in year 1, they can begin to move towards the abstract notation by recording number sentences such as 5 + 3 = 4 + 4.
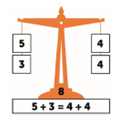
Pupils could record this pictorially through drawing the counters into a pre-made tens frame or move towards using Cuisenaire to build the numbers.
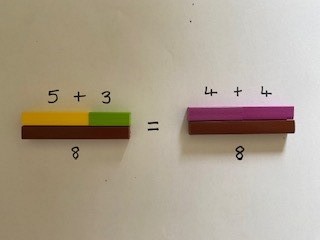
The choice to shift the resource to Cuisenaire at this point is so that pupils move from thinking about the numbers as individual ones and begin to group them together.
They can subitise 5, so the rod representing 5 deepens their understanding of unitisation – the concept that 1 unit could represent any amount.
Year 2
Then we move towards Year 2, where the numbers get bigger and pupils explore the same concept, but at a deeper level, maybe attempting problems involving missing numbers to really test their security of understanding. Once pupils understand equals as a balance, they can begin to explore Equal Difference.
The concept of difference is tricky for many pupils, often because adults very quickly jump to the end point, which is subtraction. But difference is not subtraction, it is a comparison.
To find the difference, we must compare two quantities, side by side, and see what the gap is between then two. Ultimately, children will need to see that the effect of finding the difference is subtraction, but they need to get there slowly, by going back through the CPA approach again.
To start, pupils can line up 2 small quantities such as 8 and 5. To reduce working memory at this point, it is necessary to work with single digit numbers again, so that pupils can concentrate on the strategy. Underneath they record the abstract notation 8 – 5 =

From here, encourage pupils to fill in the ‘gap’ with yellow counters and reach the answer of 3.
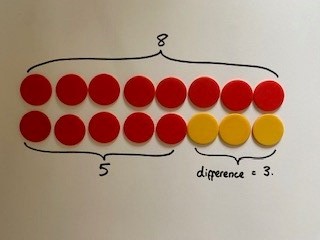
Now there is an opportunity to play around with the calculation, placing 1 more red counter onto both amounts and noticing that the difference of 3 remains the same.
9 – 6 = 3
10 – 7 = 3
11 – 8 = 3
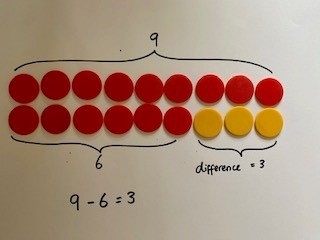
Being systematic in this way will assist pupils in seeing that some calculations are easier to solve than others. They will most likely express that 10 – 7 is easier than 8 - 5 as it is a number bond to 10.
At this point, we want to help pupils see the link between difference and subtraction, so an alternative resource such as a number line is now introduced. By lining up the 2 number lines first, to mimic the counters model, pupils can identify the difference of 3 and cut out a strip of paper to fit.
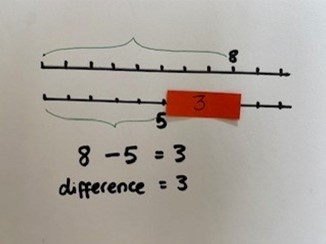
Now reduce this again on to 1 number line and place the difference in between the 8 and the 5. Write the calculation 8 – 5 = 3 and repeat, shifting the strip of paper up and down the number line to create other subtraction questions, ensuring the conversation is focused on ‘what stays the same?’ and ‘what’s different?’

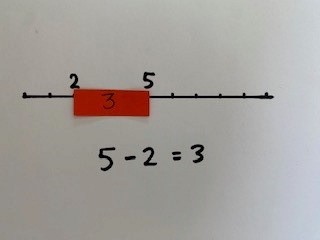
Throughout this process, there are ample opportunities for pupils to record their explorations pictorially, whether that be child-led for the counters or on pre-drawn number lines as a scaffold.
Key Stage 2
Once pupils have understood the concept of equal difference around Year 2/Year 3 and have reached the generalisation, ‘If I add or subtract an equal amount to the minuend and subtrahend, then the difference will remain equal’, this can be applied for larger numbers, increasing through Year 4 and into Year 5, where pupils may be exposed to a calculation such as 6 million subtract 4,345,576 or decimals.
Many children will attempt this question using the formal method of subtraction, which is a valid option. However, there are multiple opportunities for pupils to make errors with this strategy, as they will need to regroup in every column.
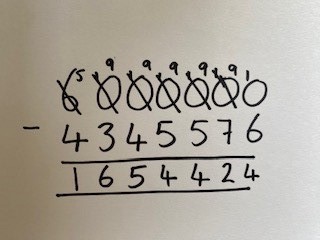
Whereas if they apply the strategy Equal Difference, they can subtract 1 from both numbers and instantly the calculation is more managable and less prone to error.

At this end point for the strategy Equal Difference, maybe around Year 4 or 5, pupils are now mostly working abstractly, but because they have worked their way through the CPA process, they have a deep understanding of the concept and as a result are able to apply to any calculation if it makes it more manageable. They have become more flexible in their approach, taking note of the digits involved in the calculation and so choosing the most efficient method.
Opportunities for the careful shift of manipulative at crucial moments occurs throughout the curriculum. In part 2 of this blog, we will look another sequence of learning, focused on learning multiplication facts, and how effective use of the CPA approach can deepen pupils understanding and aid retention.
To summarise, here are a few things to consider when using a manipulative to develop conceptual understanding:
- Where do the building blocks for the concept begin?
- What elements of CPA have already been explored for these building blocks?
- Where will the learning lead on to?
- Which resource will best exemplify the concept?
- How will you use it?
- When will it be introduced?
And most importantly…
- When will the choice of resource shift, to move pupils understanding on?
- What will the new resource be and why?
To keep up to date: Join our Primary Subject Leaders’ mailing list
To subscribe to our blogs: Get our blogs straight to your inbox



