
It feels like a while ago now but the Complete Mathematics conference for mathematics leaders and teachers in primary schools in London was only a few weeks ago. On the day, I was struck by some recurring themes and mentioned in my workshop with Gill Shearsby-Fox, some of the words that I had jotted down that I felt connected them. In the spirit of the generous collaboration that was so evident on the day, I thought I would share these, in case they help others to reflect too. I have highlighted my key word takeaways in bold below and tried to pull together these threads into wider themes.

When discussing the maths landscape and what we are noticing in our work with maths leaders, teachers and learners, I was particularly struck by 3 themes:
- relationships
- choices
- implementation
The theme of relationships was two-fold: the relationships that we have with pupils and our unwavering belief that all can be successful in mathematics and the importance of supporting pupils to see relationships within mathematics. For me, pupil relationships are inextricably linked with implementation and so I will come back to that.
Mathematical relationships
The first recurring theme of the day then, was the importance of mathematical relationships. Mathematical relationships were considered in terms of:
- building number knowledge
- considering conceptual arithmetic structure
- seeing relationships when we transfer between different CPA models
- development of calculation strategy and considered inherently within approaches to problem-solving.
Non-routine problem solving: 'I know that...I know how...I know when...'
Stephanie Taylor @TeacherTaylorS
I guess it should come as no surprise that relationships were a central theme on a day focused on mathematics education. As Stephanie Taylor reminded us so well:
“Mathematics is a creative and highly inter-connected discipline.”
(National Curriculum of England, 2013)
and so of course relationships are integral to understanding and applying mathematics.
I was particularly struck in her session on problem-solving, with the relationship between fluency, reasoning and problem solving.
Her use of a play script to be explicit in exposing this relationship was genius and I loved how you could hear the voices of problem solving (PS), reasoning (R) and fluency (Fl) as they approached, first a practical problem, and then applied this strategy development to a mathematical NRICH problem.

To infinity and beyond! Teaching mental calculation strategies for understanding.
Siobhan King @siobhanjking
Gill Shearsby-Fox @FoxShearsby
Within the workshop that Gill and I led, we focused on developing fact recall within 20 and application of this to calculation strategy to build efficiency. I guess this might have been why relationships were so firmly in my mind on the day.
The most important message that we wanted to get out there was the importance of developing relationships when building number fact knowledge to enable learning to be secured and allow the application of this to calculation strategy development further along the mathematical journey.
We noted the problems of pupils getting “stuck” at counting and the danger of pupils who move straight from counting to ‘mastery’ and rapid recall of facts, without truly considering relationships. It is only through an explicit focus on relationships that facts can be connected, and this is what enables learning to be built forward.

Teaching and learning maths with real and virtual manipulatives
Bernie Westacott @berniewestacott
Bernie Westacott’s session screamed out relationships when he considered the importance of helping pupils to transfer between different CPA models to build their mathematical understanding.
What resonated here was how crucial it is that manipulatives help children to make sense of the mathematics.
Bernie was a font of knowledge and with the focus on the day being virtual manipulatives, he was not only able to signpost where to find these and show how they could be used, but also to draw attention to the fact that it is pupil interaction with manipulatives which enables deep thinking and connection building that is key to their successful use. This is what enables pupils to make sense of the relationships between the manipulative and the abstract concept that they represent and so build a deeper mathematical understanding.
The next big thing in mathematics education?
Kieran Mackle @Kieran_M_Ed
The whole focus of Kieran Mackle’s session was arithmetic structure – the importance of understanding what the different structures are and how these can be built within curriculum sequences. Relationships were implicit in this. What really resonated here was the need to ensure that within teaching focus we explore how the structures are connected and to be explicit in exposing and using this. For example, whilst building a map of the relationships within additive structures, Kieran was able to identify how augmentation within addition is intimately connected to reduction within subtraction.
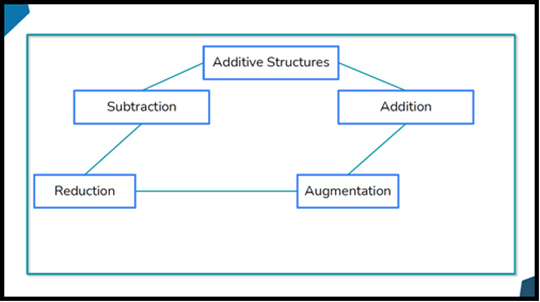
Exploring the relationships between the structures of arithmetic, enables pupils to think deeply and therefore development of a richer mathematical understanding. Importantly, explicit teaching focus on the structures also enables us to force pupils to make choices so that they think deeply about when different structures occur rather than blindly applying the operation of the day. The importance of thinking deeply about the questions we choose to drive the teaching focus struck a chord.
Choices
Kieran’s session was not the only time where choices became a theme.
Stephanie’s focus on problem-solving was underpinned by the desire to develop pupils who make choices as this is an inherent part in behaving mathematically.
In our workshop, we drew attention to the danger of pupils who do not make choices in their application of calculation strategies and who therefore do not develop efficiency in their strategy selection.
It was teacher choices that Bernie made me think about. Absolutely, he gave us a wealth of options in terms of manipulatives to choose from. But more importantly, he drew attention to the necessity to consider how the manipulatives under consideration related to the target concept so that they could do the intended job.
The importance of teachers thinking deeply about the mathematics learning and making choices to enable it to be built securely is absolutely at the root of my final theme…implementation.
Implementation
For all the curriculum design and intentions that leaders have, this will only ever be as powerful as the way in which it is implemented. Documents of intent and vision statements can only be measured in their success through the lived experiences of pupils and the impact of what happens in our classrooms.
All the conference sessions were thoughtful and practical and had effective implementation at their heart.
However, Matt Swain’s session stood out as being packed full of this focus on moving from intent to implementation.
Mastery at primary
Matt Swain @mattswain36
Based on the belief that all children can become successful mathematicians, Matt shared how practice has been developed across five schools to enable every child to succeed. My biggest takeaway from Matt’s session was his clarity of approach to closing gaps for every child and the systems and structure which have enabled this to be implemented relentlessly and with rigour.
What is needed to support teachers and to enable implementation to be successful?
A few things jumped out from references and connections between the various sessions:
- teachers who appreciate the beauty and power of mathematics and want to build a sense of enjoyment and curiosity about it
- teachers who understand mathematical ideas so that they can help make connections
- teaching that is well sequenced and builds new knowledge by enabling pupils to actively focus on it
- teachers who put pupils firmly at the centre of their learning, enabling them to embody the learning and see relationships to help them make sense of what they know, to secure it and build on it across the whole mathematical journey
- leaders who create the conditions and structure which enable all of this to happen.
Well that’s my thinking deeply about mathematics education that came from the conference. I hope that perhaps it has helped you to make some connections too.
Further reading:
Why can’t Johnny remember the basic facts?
'It ain't what you intend, it's the way it is implemented, and that's what gets results'
How can we advantage the disadvantaged?
Making Fluent and Flexible Calculators Project

Express an interest in joining the next round of the Making Fluent and Flexible Calculators Project.
To keep up to date: Join our Primary Subject Leaders’ mailing list
To subscribe to our blogs: Get our blogs straight to your inbox






