
I spend most of my time in primary schools but sometimes, I have the opportunity to visit KS3 classes. When visiting a Year 9 class recently, I observed students completing algebraic equations. They demonstrated good understanding of what they were doing and happily talked to me about their learning. I then noticed that several of the students were able to do the complex algebra but couldn’t add two single digits without using their fingers. Since observing this, I have noticed it more and more; children being able to do the ‘maths’ but needing their fingers to solve simple calculations.
The next question is, does this matter if they understand the maths they are learning?
I would argue that it does. Lack of fluency in base facts slows most maths learning.
The Ofsted Research and Analysis Review into mathematics (May 2021) recognises the need for fluency in base facts and the impact of not knowing them.
“Pupils who are not able to quickly and easily recall maths facts struggle with calculations due to their working memory being overloaded. For example, a child who does not know number bonds will be stuck using various forms of ‘counting on’ when performing simple addition.”
I have recently had the pleasure of developing the ‘Making fluent and flexible calculators’ project with Charlie Harber and Siobhan King. In Charlie’s recent blog, she clearly shows the importance of teaching pupils to build on their knowledge of the base facts to make connections and spot patterns. So far, we have seen great impact on the pupils taking part in the project with pupils making the equivalent of 8 months progress in just 6 weeks.
One teacher involved in the project stated:
“Children are not scared anymore of numbers and doing the mathematical talk in front of their peers.”
Despite this, I also know that there are a few pupils, usually in the bottom 5%-10% or who have special educational needs, who are never very clear about the maths they are learning and very rarely feel success. Many of these pupils have ‘survival’ strategies – cleverly masking what they don’t know – or are overly scaffolded by adults. Teachers are aware of these pupils; they identify them as pupils who never seem to retain anything. Teachers feel there is a pressure to ensure all pupils access the same learning. They want to help but don’t know where to start; it can be overwhelming and the journey back to age related expectations too long and bumpy.
So, what should be done?
Base facts need to be secured with conceptual understanding – explicit teaching of strategies. As it states in the maths review, if pupils don’t know their base facts, they can get stuck on counting strategies.
This short video explains Baroody’s phases to automaticity and explains why teaching the facts with strategies is so important.
Teaching strategies
The base facts to 10 + 10:
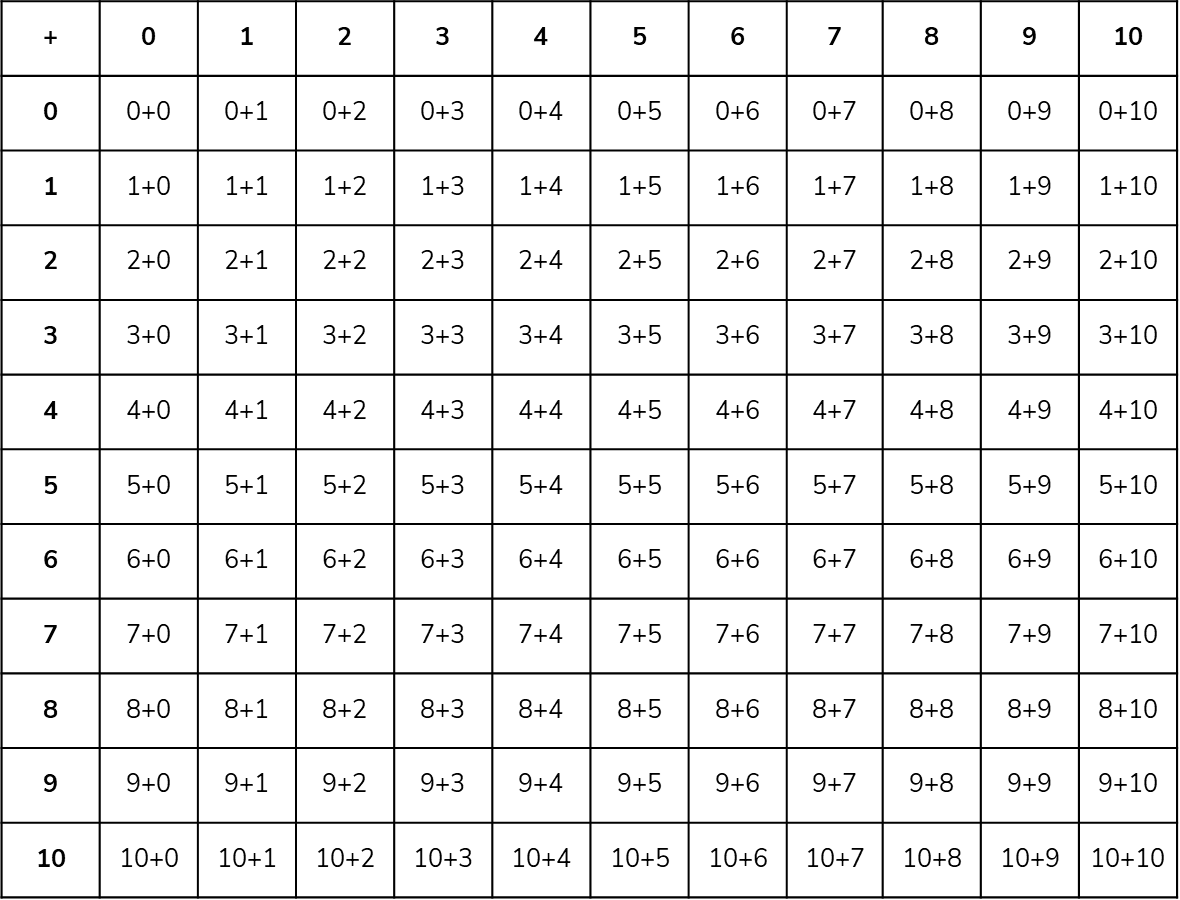
We have identified 9 different strategies within the base facts. This video explains them:
We now know the strategies that are needed to learn the base facts, so the next challenge is:
How do we know which strategies children know and which ones they don’t?
The HFL Education maths team have created a short diagnostic assessment to be used one to one with pupils to find out how pupils calculate answers. With this diagnostic assessment, it is not the accuracy of the answer that is important; it is the efficiency of the strategy.
Below are some examples of pupils solving calculations from the diagnostic assessment.
All the answers are correct, but you can probably tell from the dots and dashes drawn that ‘counting all’ was the only strategy that was used.
Thinking about the different strategies listed in the video, what would be more efficient?
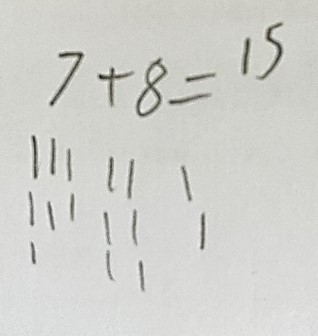
7 + 8 = 15
Using knowledge of doubles ( 7 + 7 or 8 + 8 ) to calculate this would increase efficiency; they would also need to apply knowledge of one more or one fewer to find the near double.
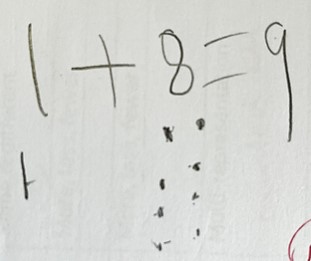
1 + 8 = 9
Understanding the commutative nature of addition helps. Applying this means that the addends can be swapped and the calculation read as 8 and one more.
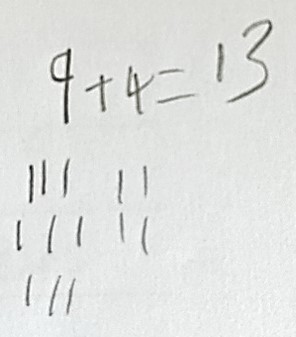
9 + 4 = 13
Recognising that 9 is near 10 aids calculating this. The 9 can become 10 and 4 more added to make 14 and then adjusted by 1 to get 13.
Or 1 can be taken from the 4 added to the 10, to think 10, and the remaining 3 then added.
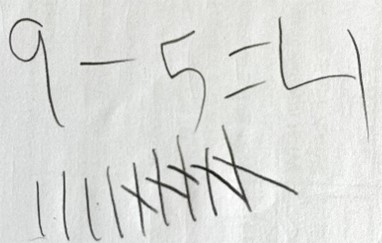
9 – 5 = 4
When learning base facts, the inverse facts also need to be learned and for this calculation, the knowledge of 5 and some more is helpful. If it is known that 9 is 5 and 4 more, when subtracting 5 from 9, this knowledge can be applied.
What could the explicit teaching of the strategies look like?
Once the strategies children know or don’t know have been identified, teaching of unknown strategies can happen and base facts can be learned.
This video provides some ideas for how strategies could be taught and rehearsed:
The HFL maths team are in the process of completing developmental research on a short, sharp intervention – Mental maths fluency intervention – that focuses on identifying and teaching base facts. Initial trials completed this year have been positive with the schools involved seeing much improved knowledge and application of base facts.
Download a free sample of the teaching guidance from the Mental Maths Fluency Intervention here:
To keep up to date: Join our Primary Subject Leaders’ mailing list
To subscribe to our blogs: Get our blogs straight to your inbox
References
Research review series: mathematics - GOV.UK (www.gov.uk)
Baroody, A. J., Bajwa, N. P., & Eiland, M. (2009). Why can't johnny remember the basic facts? Developmental Disabilities Research Reviews, 15(1), 69-79. Why can't Johnny remember the basic facts? (wiley.com)



