
Why bother to teach mental calculation strategy to solve 9 + 5? Does it matter if the only way a child can solve this is through using the ‘counting on’ strategy? Isn't it more important that they get an accurate answer?
Yes, it does matter that they have other ways to solve this simple calculation.
For a Year 2 child, the difference in time to solve 9 + 5 through ‘counting on’ or employing another mental strategy (such as rebalancing the calculation to 10 + 4) would be minimal. However, when the same child is presented with a situation involving them solving 49 + 35, the difference in processing time increases significantly. Confidence in attaining the accurate answer could be higher (rebalancing would allow 49 + 35 to become 50 + 34).
When presented with a calculation, children will apply the strategy that has been the most successful for them. If they have previously been using ‘counting on’ and got their reward tick, that will confirm to them that the most important part of the calculation is to get the correct answer. I am not arguing that the correct solution is not important; it really is, but it’s not the only part of the process we should show the children that we value.
The problems start when the calculations involve two-digit numbers, then three-digit numbers, then decimals, and they still default to this method. The volume of data to process has increased significantly. The difference in processing time between the count on and a more efficient mental strategy has now become critical.
Let's look at the volume of data they are dealing with if they try to solve the two different calculations. When solving through the count on or indeed the count back strategy, the children are doing a 'double count', meaning that they need to know how many counting steps (or acts) they have to do (which they usually track on their fingers) and also where in the number sequence they are on each count.
Figure 1 shows an example of how a child might solve 9 + 5 using the count on strategy.
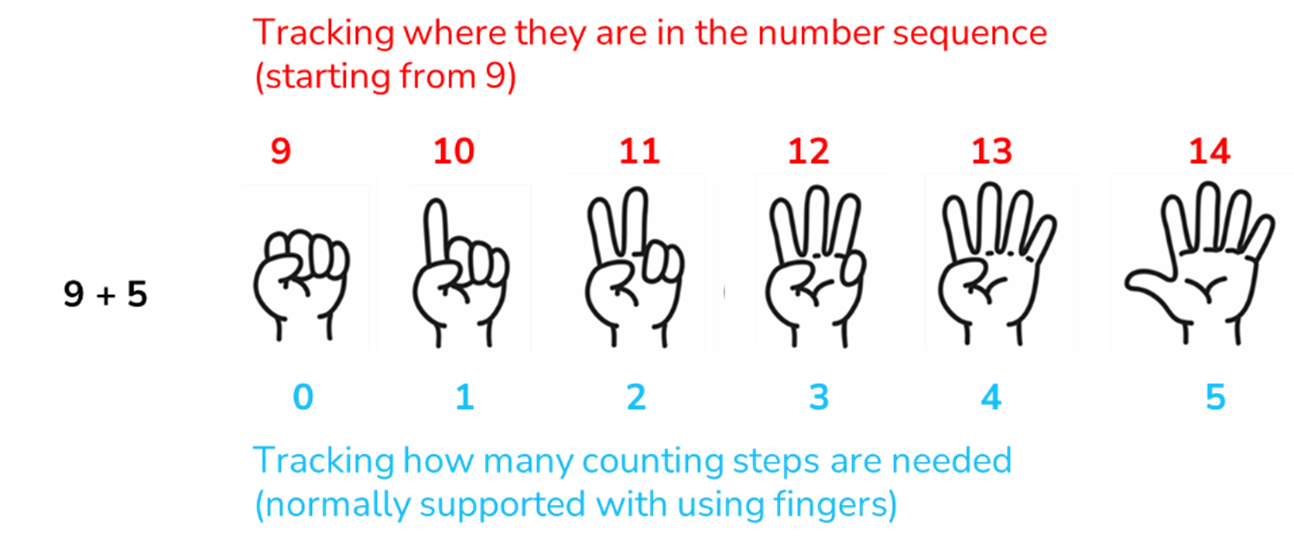
So far, so good; they have enough fingers to track the count, so the counting act doesn't take too long. In this case, the count on strategy would be appropriate for the children to use.
But what happens if the child tries to apply the same strategy to 49 + 35?

How will they keep track of how many counting steps they must do and how far along in the number sequence they are? They might be able to keep track on their fingers, but they will then also need to keep track of how many times they have gone through all ten fingers. They might try to verbalise the double count.

It becomes challenging to keep track of what the two counts represent and children start to get confused or skip steps in either, or both, of the counting sequences.
The volume of information for many children becomes overwhelming, leading them to become frustrated and ultimately give up, generating negative feelings and lowering self-esteem.
Mental calculation is not “being able to do the sum in your head”. It is not defined by the ability to solve a calculation without making any jottings or notes.
It is about helping children spot patterns and look for meaningful relationships between numbers, and enabling them to creatively use these to simplify calculations.
As our children pass through primary school, we need them to build strong foundations in maths. We must help them create meaningful mental images that can be manipulated and employed flexibly and creatively.
Strong mental maths skills are essential for children to develop.
They:
- build a strong conceptual understanding of numbers and mathematical relationships;
- boost confidence and self-esteem;
- stimulate curiosity and forge positive relationships with maths;
- exercise the brain;
- are used extensively in our everyday life;
- are a gateway to more complex mathematical concepts.
Dr Abadzi, a cognitive scientist at the University of Texas, states that ‘people are basically prisoners to their working memory’.
During the Making Fluent and Flexible Calculators project, I have often seen clear examples of children being prisoners of their working memory, trying to hold too much information at once. I have seen them trying to keep the double count in their heads, using their fingers to track the count, tapping the table with their fingers, and using tracking jottings (see figures 2 and 3).
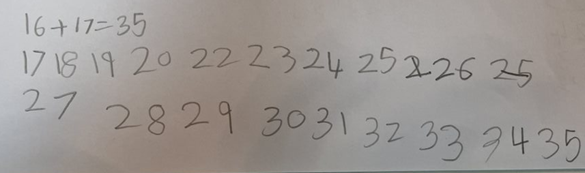
Figure 2 shows a child's work showing ‘count on’ tracking jottings to solve 16 + 17 with common errors.
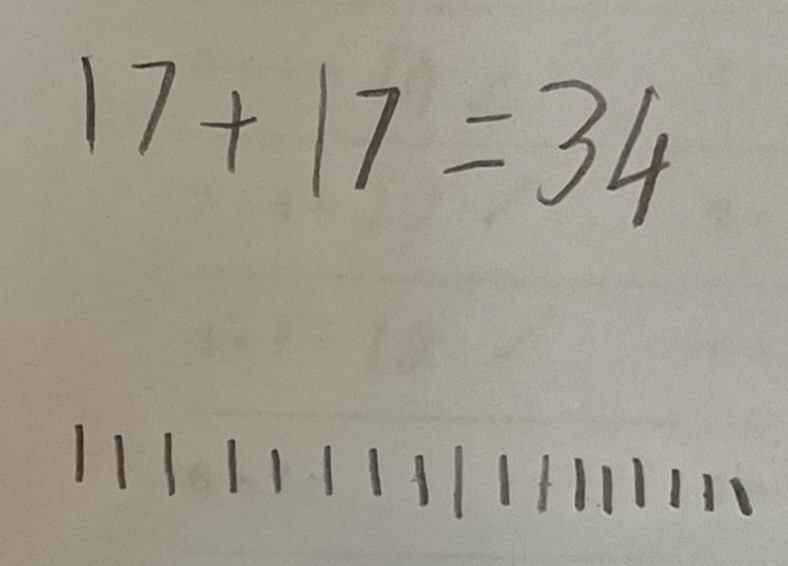
Figure 3 shows an example of a child's work showing ‘count on’ tracking jottings.
When Making Fluent and Flexible Calculator: whole class intervention teachers have assessed their classes of children, they have consistently been surprised by the high percentage of children who are still solving problems through ‘counting on’. The inappropriate application of ‘counting on’ or ‘counting all’ significantly limits their ability to engage in more complex calculations, including multiplication and word problems, as their working memory becomes cluttered.
In the absence of confidence and practice in other mental strategies, knowing and using base facts (chunked-up information which takes up less space in the working memory), the cognitive load is immense! Imagine the load when they try to do more complex calculations. They are indeed prisoners of their working memory and caught in the counting trap.
Introducing children to a range of mental strategies early (calculations involving single-digit numbers) allows them to explore them with concrete resources and more clearly see how and why the strategies work. They can find early success with various strategies.
Through early engagement in reasoning about strategies, they will understand that the strategy is of value and that they have agency over which strategy they employ and can manipulate the numbers to make more ‘friendly’ calculations, lessening the cognitive load and being playful with their mental maths.
Making Fluent and Flexible Calculator: whole class intervention is a whole class project which supports pupils to:
- develop and use base facts;
- engage in exploring a range of mental strategies;
- develop fluency through well-designed practice and fluency sessions;
- have fun and become curious about number patterns.
This project is something that all Lower Key Stage 2 teachers should engage in to enable children's ongoing success and a genuine love of maths.
Express interest in finding out more or taking part in the next round of the project here: Expression of interest form.



