
In the first of this mini-series, (Making fluent and flexible calculators: why counting is not enough), I reflected on the importance of taking a deep look at how children solve simple addition and subtraction calculations. I considered why it wasn’t enough just to let them solve simple calculations through counting and the need to stop children from being caught in the counting trap.
This time, I have turned my attention to understanding why gaps in developing additive reasoning lead to difficulties later in children’s longer maths journey. I return to my crucial statement - 'Why getting the calculation correct is not enough’. But this time, I consider why we must blatantly pay attention to additive reasoning. If children in your class struggle with multiplication, division, fractions and/or percentages, they may not have already secured the strong foundations in additive reasoning that they need.
Shortly after publishing the first blog in this mini-series, Ofsted released ‘Coordinating mathematical success: the mathematics subject report’ (July 2023). As one of the main findings for primary schools, they highlighted:
“Pupils’ gaps in knowledge tend to be centred around, but not limited to, addition facts in younger year groups. This was for some, but not all, pupils. These early gaps in knowledge may not become apparent until a significant amount of time has elapsed. This is because it is possible, in the medium term, for pupils to understand what is being taught and then keep up with extra classroom support and slower calculation. However, this is at the expense of the later ability to access the curriculum.”
Additive reasoning is foundational to multiplicative reasoning
I have long questioned why some children seem able to move into KS2 maths easily and others struggle, particularly with multiplication.
Why am I talking about multiplicative reasoning when Making Fluent and Flexible Calculators explores, develops, and enhances children’s ability to solve addition and subtraction calculations?
It is because additive reasoning forms the foundations for developing multiplicative reasoning (see Figure 1 below). During the course of the project, we have repeatedly seen large proportions of pupils using counting to solve simple addition/subtraction calculations. They have yet to develop trust in a range of strategies and haven't developed the habit of looking for ways to simplify the calculations. Instead, they revert to counting or, slightly better, depend on a single strategy (for a more detailed discussion on the strategies children spontaneously use in the project, see the first blog in this series)
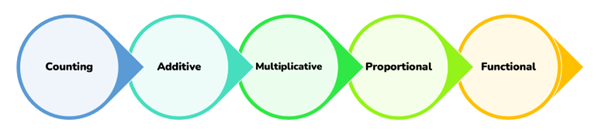
Figure 1: Reasoning progression phases from EYFS to KS4 and beyond
Each phase is progressive, building understanding and knowledge vital for success in the next phase. To be blunt, if a child doesn't secure the required learning in the additive phase, they will struggle with the multiplicative.
Too many children are trying to solve multiplication calculations with understanding and knowledge only from the counting phase. This is why some struggle to understand and accurately answer multiplication questions and find proportional reasoning, such as fractions, percentages, and ratio, ‘a bridge too far’.
To illustrate this, consider what happens when children solve 9 x 6 when this fact is not fluently recalled:
Child A
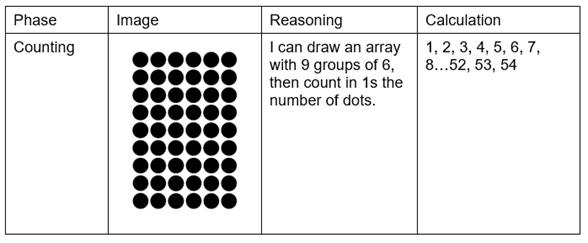
Child A is in the counting phase, so they solve the calculation by drawing an array; nine rows with 6 dots in each. Then they count each dot, starting from 1 (count all) or, slightly better, from 6 (count on).
Child B

Child B is in the additive phase and solves the calculation through skip counting. They now recognise that there are 9 groups, and each group is equal to 6. They no longer see each item (dot), but rather 9 repeated equal units of 6. They solve through applying repeated addition, so even though they are solving a multiplication calculation, they are employing strategies from either the counting or additive phase.
Child C
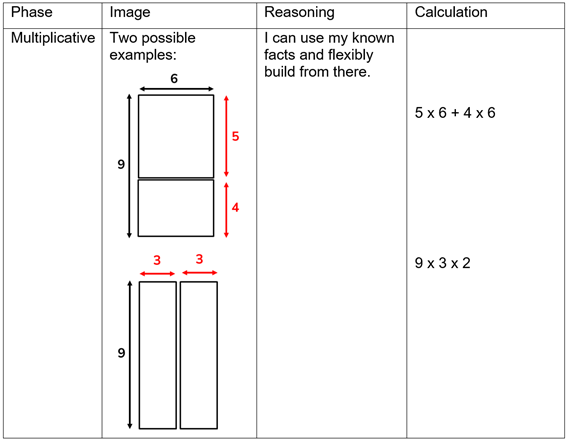
Child C’s solution is representative of the multiplicative phase. They have developed an understanding of the two different dimensions of multiplication - the number of groups and the size of groups. They can flexibly manipulate both dimensions to break the multiplication into groups to which they fluently know the answers. They must employ skills from both the multiplicative and additive phases to succeed at this stage.
In addition to the macro-progression of counting to additive to multiplicative, each phase has a micro-progression
Children start with unitary counting; counting all the dots, one to one. This strategy is not time efficient and has massive potential for error. They do not see the array as representative of multiplication or the relationships between two differing dimensions (number of groups/size of group) but rather just a series of single dots. The child’s ability to estimate if their answer is correct is minimal.
Rhythmic counting is how many children first solve multiplication calculations when they start to recognise groups; they emphasise the number pattern but are still counting in ones. When counting in sixes, they would whisper 1, 2, 3, 4, 5, and shout 6, whisper 7, 8, 9, 10, 11, shout 12 and so on. They recognise the repeated addition structure but still employ skills from the counting phase.
As children get more confident with rhythmic counting, they can often skip count some of the patterns but then revert to rhythmic counting to complete the calculation. This is called ‘hybrid counting’. For example, 6, 12, 18, 24, 30…whispering 31, 32, 33, 34, 35, call out 36; whispering 37, 38, 39, 40, 41, call out 42, etc.
The cognitive load is huge when using this method as children must keep track of numerous pieces of information all at once, including:
a) the number of groups of 6 that they have counted
b) which number they are currently on
c) which number comes next in the number sequence (particularly challenging if it crosses a decade boundary)
d) how many more they must count on to complete the next group of 6.
However, if children are confident in additive reasoning, then they can start to simplify the repeated addition calculation and compact the amount of information they are processing, releasing cognitive space. A child’s thinking might be:
I know 5 x 6 is 30, so 30 + 6 = 36, 36 + 6 = 42, 42 + 6 = 48, 48 + 6 = 54.
During this intermediate stage, children use additive reasoning strategies to solve the sub-calculations required to multiply 9 and 6:
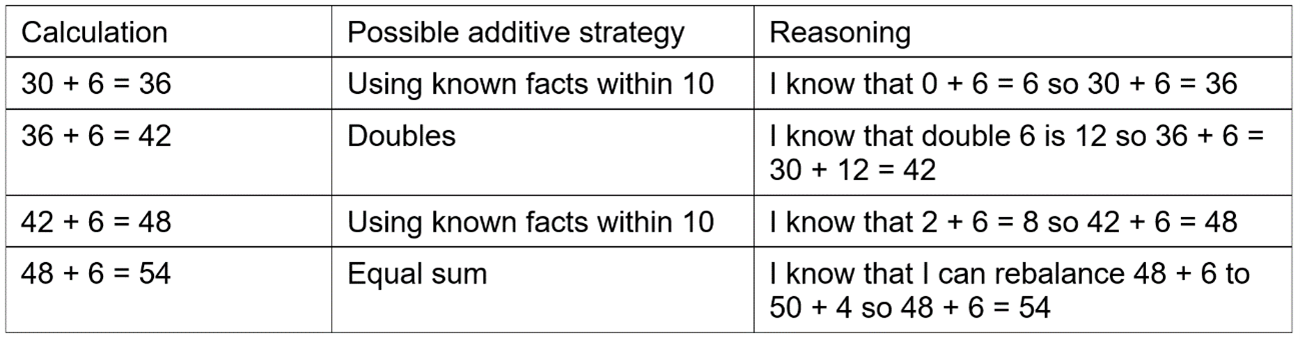
Ability to use base facts
In the first blog in this series, I discussed the importance of children developing mental addition and subtraction strategies to prevent them from being stuck in the counting trap.
But the ‘Fluent and Flexible’ project has also highlighted another issue. Thompson (1994) highlighted that children must understand that mathematics is about “working with relationships”.
The entry data from the project shows that many of the children aren't spontaneously using their base facts to help with other calculations (the National Curriculum refers to them as ‘derived facts’). Children do not see relationships between calculations and are not using what they already know.
For example, suppose pupils know that 9 + 4 is 13. It is then anticipated that they would use this information flexibly to solve other related calculations, such as 90 + 40, 19 + 14 and 13 - 9, but we found that many children involved in the project weren’t. Instead, they see all calculations in isolation. They aren’t in the habit of anticipating and seeking ways to make the calculations easier using known facts.
Not seeing associations between calculations has implications for their longer journey in maths. Children need to build the habit of seeking patterns and seeking ways to simplify calculations in preparation, not just for more complex additive calculations, but also multiplication (if I know 3 x 4 is 12, then 30 x 40 is 120, 13 x 4 is 10 x 4 + 3 x 4). Children need explicit instruction, time, and practice to seek and trust relationships.
Moving beyond known multiplication facts
The ability to use additive strategies is much more than just being more efficient within the times tables facts. As they progress through the curriculum, children will have to use additive reasoning to solve calculations beyond their known multiplication fact range.
Additive reasoning impacts multiplication success
To summarise, additive reasoning develops this kind of understanding and knowledge:
a) numbers can be broken into smaller numbers (composite units/part-whole models)
b) how to use base facts to seek derived facts – going beyond memorised facts
c) to select, with reasons, from a range of strategies to simplify the calculation.
In the 2023 Key Stage 2 mathematics paper 1: arithmetic, there were 15 questions that explicitly involved multiplication or division (excluding those that contained fractions). Of these, at least 9 can be simplified and solved using additive thinking strategies.
Examples include:

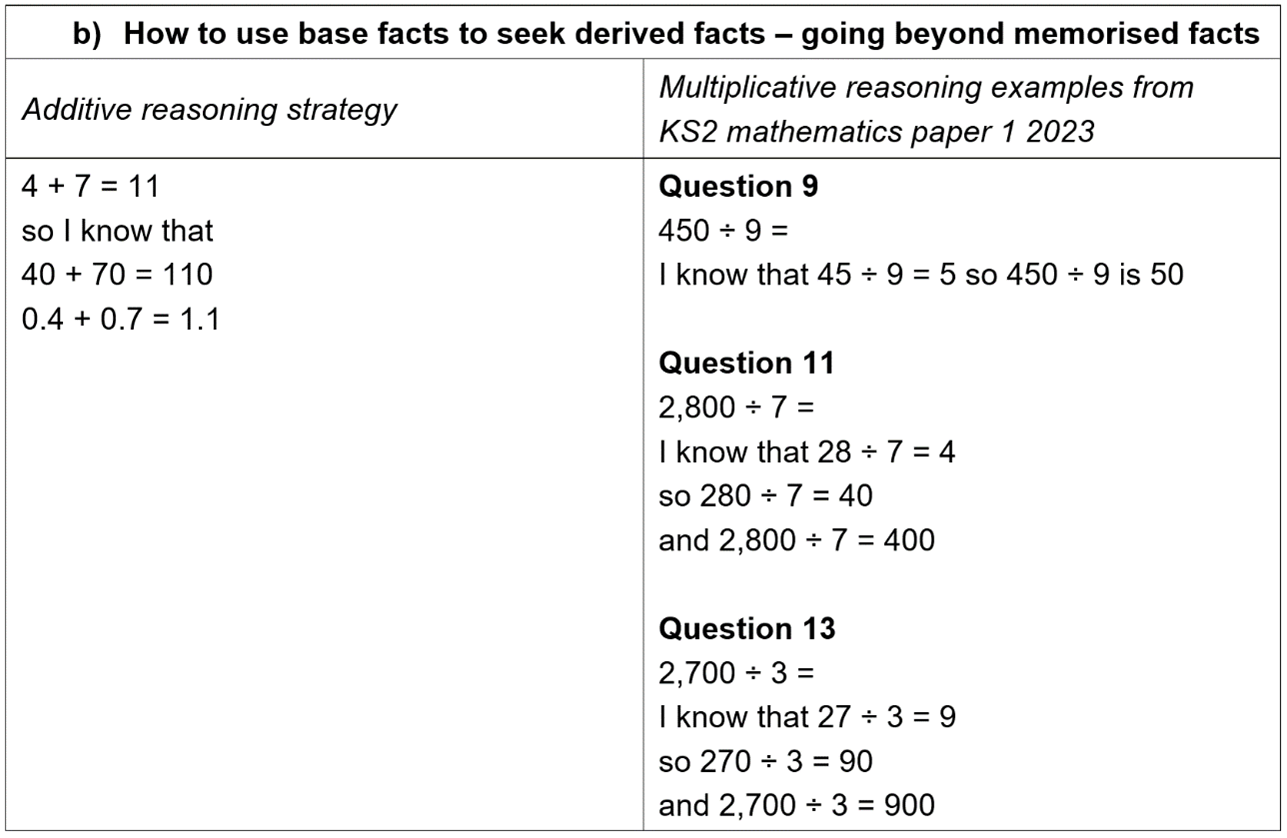


That there are many ways to solve each calculation is critical here. It is up to the children to decide. They have the agency so select the option which exploits their strengths.
We need to explicitly help them establish the habit of seeking patterns, build their understanding and trust in additive reasoning so that they will continue to look for relationships within and between numbers. This will help them to learn to seek out ways to simplify calculations rather than mechanically applying the same strategy over and over again.
This foundational flexibility enables them to build more sophisticated ways of solving calculations, preparing them to be successful with more complex calculations.
It is vitally important that we aren’t satisfied with children getting simple addition and subtraction calculations correct, but that we overtly focus on the strategies and the understanding that the child is applying. We should constantly question ‘are they building foundations to enable success for the next stage of their maths journey?’
Is this a key focus in your school?
The HFL Education Primary Maths team can work with you in school to develop mathematical fluency through The Fluency Package or the teaching and learning of multiplication facts through The Multiplication Package.
Find out more about the Making Fluent and Flexible Calculators
To keep up to date: Join our Primary Subject Leaders’ mailing list
To subscribe to our blogs: Get our blogs straight to your inbox
References
2023 Key Stage 2 mathematics paper 1: arithmetic
Contains material developed by the Standards and Testing Agency for 2023 national curriculum assessments and licensed under Open Government Licence v3.0
Ofsted (2023) Coordinating mathematical success: the mathematics subject report Available at: www.gov.uk/government/publications/subject-report-series-maths/coordinating-mathematical-success-the-mathematics-subject-report
(Accessed: 31 August 2023)



