
By the time this blog hits your screen, there will be approximately 26 teaching weeks until this year’s KS2 SATs tests. If you are teaching maths daily, that’s around 130 maths lessons to cover all the new year 6 learning and to revisit, retrieve and secure the rest of the KS2 curriculum. When you look at the numbers, time is tight.
Yet this precious time can get consumed by testing regimes in a bid for children to familiarise themselves with the test in the hope that their scores will improve with each new test they do. In the recent Ofsted maths subject report, the summary of the research review relevant to assessment stated:
Most schools used end of key stage tests, or similar papers. The most positive approaches kept things ‘low key’ and avoided repeated summative testing to ‘show progress’
'Coordinating mathematical success: the mathematics subject report’ (Ofsted, July 2023)
As educators, we have likely all experienced the frustration of teaching something, feeling positive about the children ‘getting it’ to then be presented with blank faces when their understanding is tested or they are required to apply this knowledge in a problem solving context.
Teaching approaches to problem-solving is just as much a part of a strong curriculum as teaching the maths which problem solving calls on. In fact, it should be an integral part of the teaching and learning process.
According to Polya’s four-step model (1957), learners progress through four stages when faced with a problem:
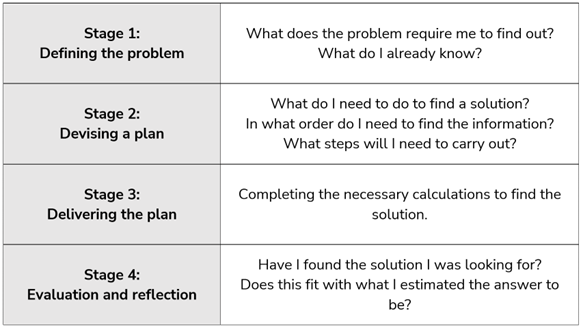
It is important that we model to the children the thought that gets us into a problem by slowing down the problem-solving approach and making the reasoning behind it explicit.
How can we teach the skills of reasoning and problem-solving?
Let’s consider how this may look in the classroom using a question from the 2023 key stage 2 mathematics Paper 3 (reasoning):
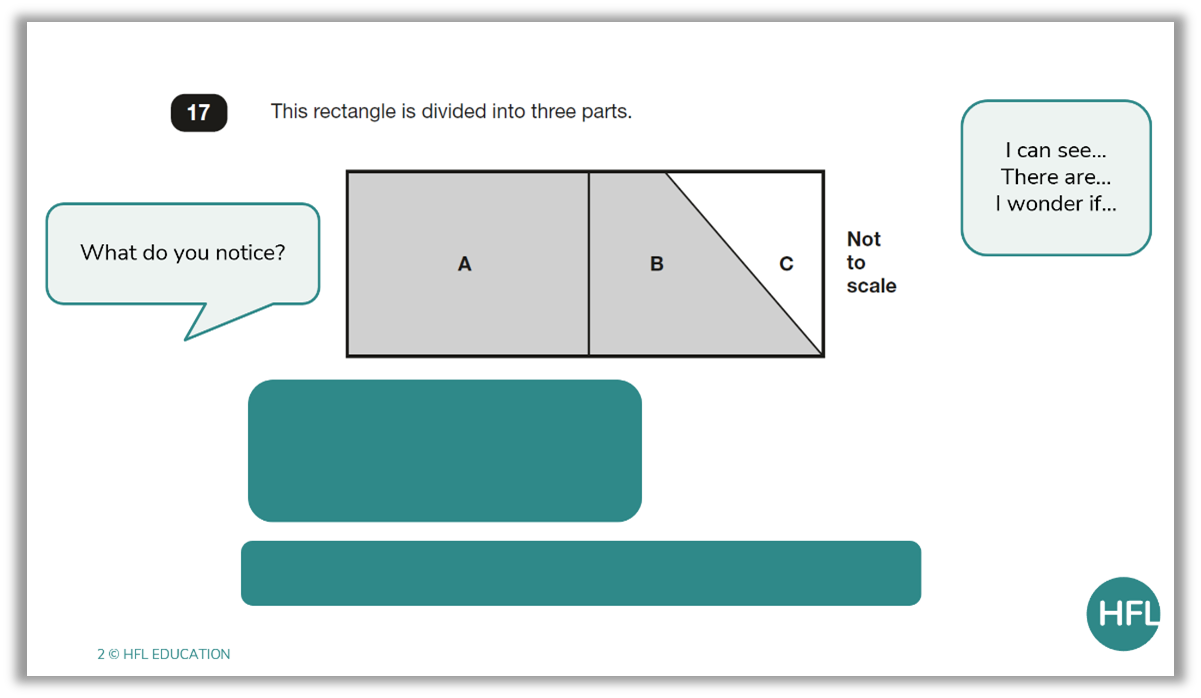
First, pupils should be encouraged to look at the models and information they have been given.
By removing the question, we are encouraging them to identify what they already know and to ask questions of what they have been shown.
Not only will this support them with noticing the maths and making connections, but it will also serve as a useful tool when they progress to stage 4 in Polya’s model and are reflecting on their solution.
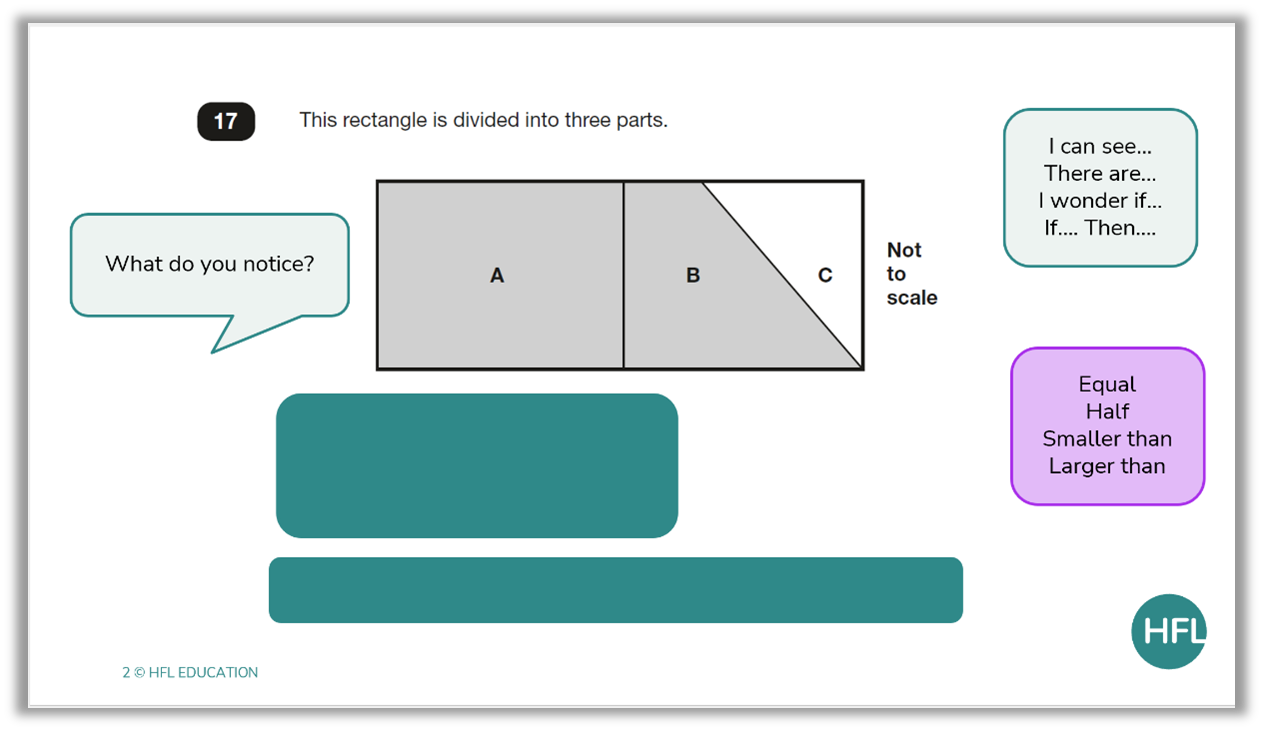
Next, we can start to refine the thinking of the learners by considering what vocabulary we would like them to be using when discussing the model provided. This signposts them to what they should begin to recognise.
The use of speaking frames supports the expectation of full sentences and analysis. At this point, you may ask pupils to consider what their peers have noticed, question it and build upon it: ‘If that’s true then…’.
By modelling to the children how we would filter the question and relate it to concepts, we begin to provide a tool for them to do this independently.
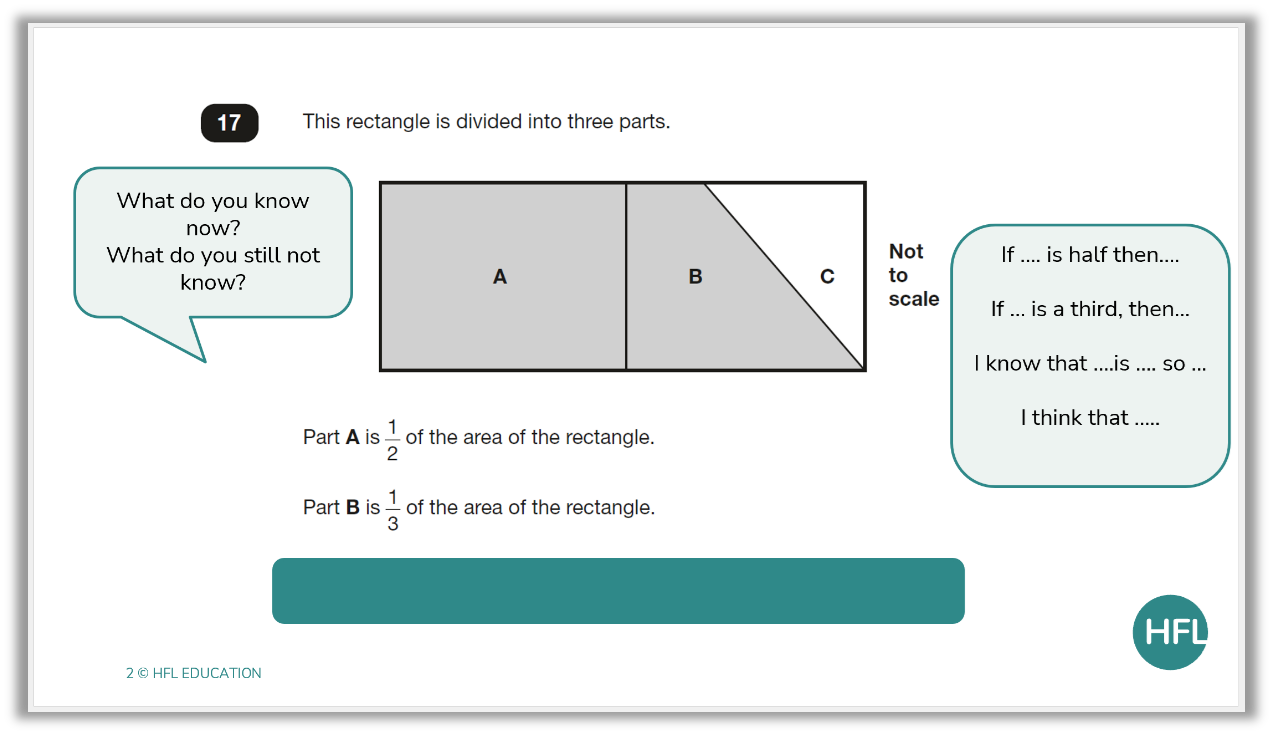
Once the children have had the opportunity to find the maths and consider what they know from the image, we can reveal some more information for them to explore.
This is where they can begin moving into stage two of Polya’s model. They know what they know and what they don’t and now they can consider how to use this to devise a plan.
At this stage, you could ask the children to consider:
- How could we present this using a bar model?
- What questions do you have?
- What calculations could give you more information?
- What could the final question be?
This scaffolds the problem solving process and enables the pupils to have a far richer discussion around the question than simply solving it under test conditions. At each point in this process, we are reducing the number of possibilities for the solution which again supports the final stage of reflection.
Finally, we reach the big reveal.
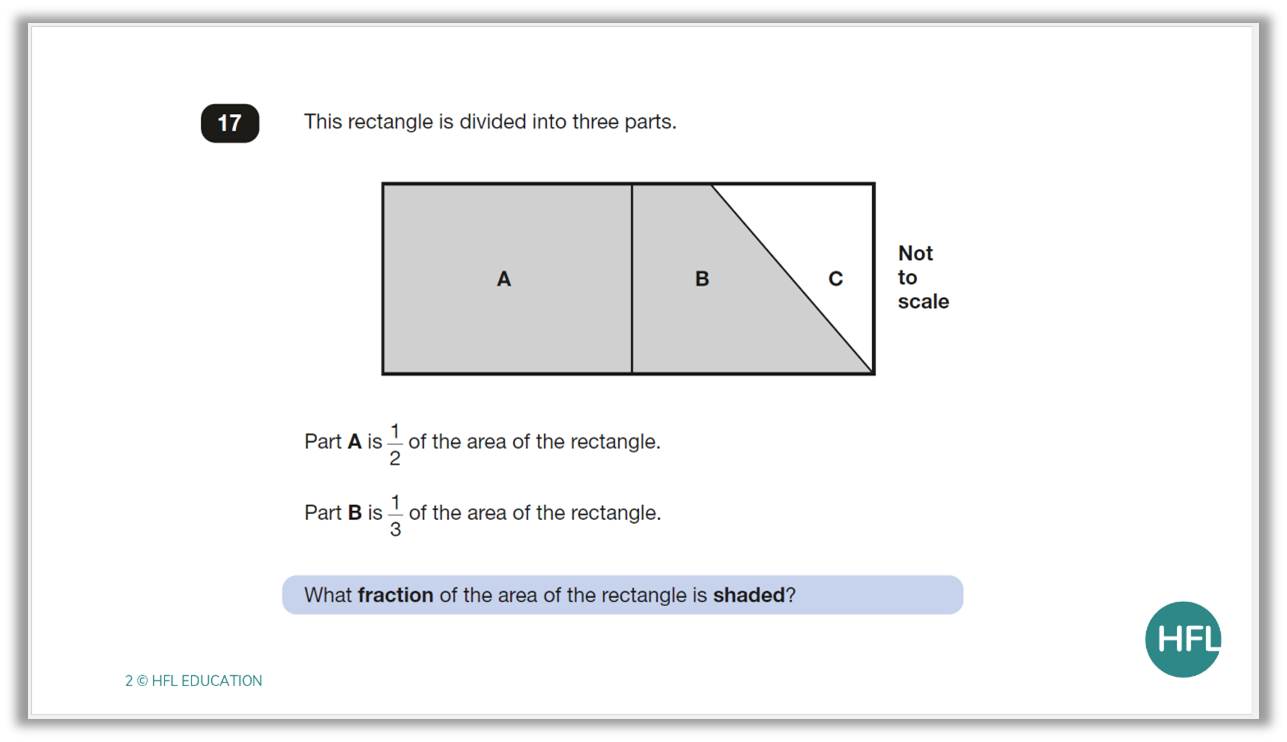
By the time we have shown them the problem in its entirity, children would have already unpicked what is required of them and feel more confident to tackle the calculation.
You may then simply ask them to solve the problem and could even extend their thinking by asking:
- How would you change the question to make it more challenging?
- Could you represent the maths using a concrete resource (e.g., Cuisenaire)?
- Could you represent the problem using two different models?
What does teaching offer that testing doesn’t?
When used on a regular basis (in place of continual testing), this approach will serve to familiarise the children with KS2 SATs test structure but also develop and enhance all children’s problem-solving skills in a collaborative way. This could be incorporated into fluency sessions, at the beginning of maths lessons or intertwined with lessons where the content is relevant.
Teacher modelling and rich discussion between peers will enable children to make links across the curriculum, support them to notice where connections can be made to what they know and develop their ability to decide what they need to find out and how. We want this to become part of their natural response when applying their knowledge and skills within a problem-solving context.
Upcoming training for Year 6 teachers
For practical, face-to-face training in Reaching the expected standard in year 6 maths, join us at the Hertfordshire Development Centre in Stevenage, Hertfordshire, on the 19th of October 2023. Use the link above to find out more. Booking is now open.
We can teach these problem-solving skills throughout children’s time at school
This strategy for exploring problems is useful not only in Year 6, but as a tool to support the development of these skills across key stage 1 and key stage 2.
By using images from real-life contexts, we can expose children to mathematical thinking and continue to build upon this as their schemata grow.
Below, you will find an example of how the problem-solving approach could look in Year 1.





The HFL Education primary maths team have developed a set of these real-life reasoning slides. Look out for further information about them in our monthly newsletters.
Subscribe to receive these direct to your inbox: Join our Primary Subject Leaders’ mailing list
Find out more about the HFL Education Curriculum Impact Packages
To subscribe to our blogs: Get our blogs straight to your inbox
References
2023 Key Stage 2 mathematics paper 3: reasoning
Contains material developed by the Standards and Testing Agency for 2023 national curriculum assessments and licensed under Open Government Licence v3.0
Ofsted (2023) Coordinating mathematical success: the mathematics subject report available at: https://www.gov.uk/government/publications/subject-report-series-maths/coordinating-mathematical-success-the-mathematics-subject-report (Accessed: 19 September 2023)



