
Looking to inject a little festive fun into your fluency sessions this month?
If you are, you’ve come to the right place!
“Oracy can be best defined as: ‘Articulating ideas, developing understanding and engaging with others through speaking, listening and communication’.
For example, in mathematics, pupils might use talk to recall and apply declarative knowledge, to model and practice thinking aloud and to justify mathematical proofs.”
‘We need to talk’, Oracy Education Commission, October 2024
This compilation of challenges has the potential to generate plenty of mathematical discussion in your classroom.
The challenge below presents an opportunity to explore equality and to rehearse number bonds and addition and subtraction strategies; all of which are vital building blocks for learning yet to come.
Begin with curiosity
What can you see? What do you notice?
Children may comment on the number of boxes on each sleigh or their arrangement. They may notice the possibility of using a familiar bond to 10. Do children notice that for two of the sleighs, there are multiple possibilities?
Valuing each contribution, as children share in their own words, is important. We can inject more accurate mathematical language later once children’s initial thoughts have been shared and listened to by the class.
Scaffold for discussion, reasoning and problem-solving
Following this initial discussion, children could work in teams to talk through possibilities and strategies to solve the problem. Arming children with pens, paper, sticky notes, useful manipulatives and simple sentence frames could provide a scaffold on which to build ideas. Sentence frames could include:
I have noticed…
If… then…
For the middle sleigh:
I have noticed that the boxes on the front total 15.
If one of the boxes at the back had 3 toys inside, then the other box would need 12 toys to equal 15.
I have noticed a pattern. The boxes could contain 1 and 14 toys, 2 and 13 toys, 3 and 12 toys…
For the final sleigh:
I have noticed that the empty box at the front needs to contain one more toy than the total toys put in the two empty boxes at the back. This is because 12 and 11 have a difference of one.
Suggestions for additional scaffolding
| Heuristics | Manipulatives | Word bank |
Create a table / spot a pattern Try then improve Work backwards | Tens frames and counters Numicon | Total Sum Equal Parts Whole Difference |
Begin with curiosity
What can you see? What do you notice?
Children might see products from familiar times tables and notice that they are not in their usual order. They might spot prime and square numbers and spot that some numbers appear more than once.
Before attempting to solve the problem, it’s crucial that children understand the design of the table – how the factors in the green row and column are linked to the corresponding products in the table.
Scaffold for discussion, reasoning and problem-solving
Following this initial discussion, children could work in teams to talk through possibilities and strategies to solve the problem. A large version of the grid, a pencil, rubber, and a beadstring could support in solving this problem.
Where times tables are not known, a beadstring would be a useful manipulative. For example, children could drag across 40 beads and use them to identify the possible factors – equal groupings of 2, 5, 8 or 10 (within the factors allowed in the problem). Sentence frames could include:
I have noticed…
It couldn’t be…
It could be…
If… then…
For example:
I have noticed that the fully blue column contains four multiples of 4. The factor at the top of the column could be 4. It couldn’t be 2 because 2 x 18 = 36 and 18 isn’t allowed.
I have noticed a square number – 100. If 10 goes at the top of the column for 100, then the factor at the end of the horizontal blue row must be 2 because 10 x 2 = 20.
Suggestions for additional scaffolding
| Heuristics | Manipulatives | Word bank |
Work backwards Solve a simpler but related problem | Beadstrings | Factors Multiples Product Equal groups |
Begin with curiosity
What can you see? What do you notice?
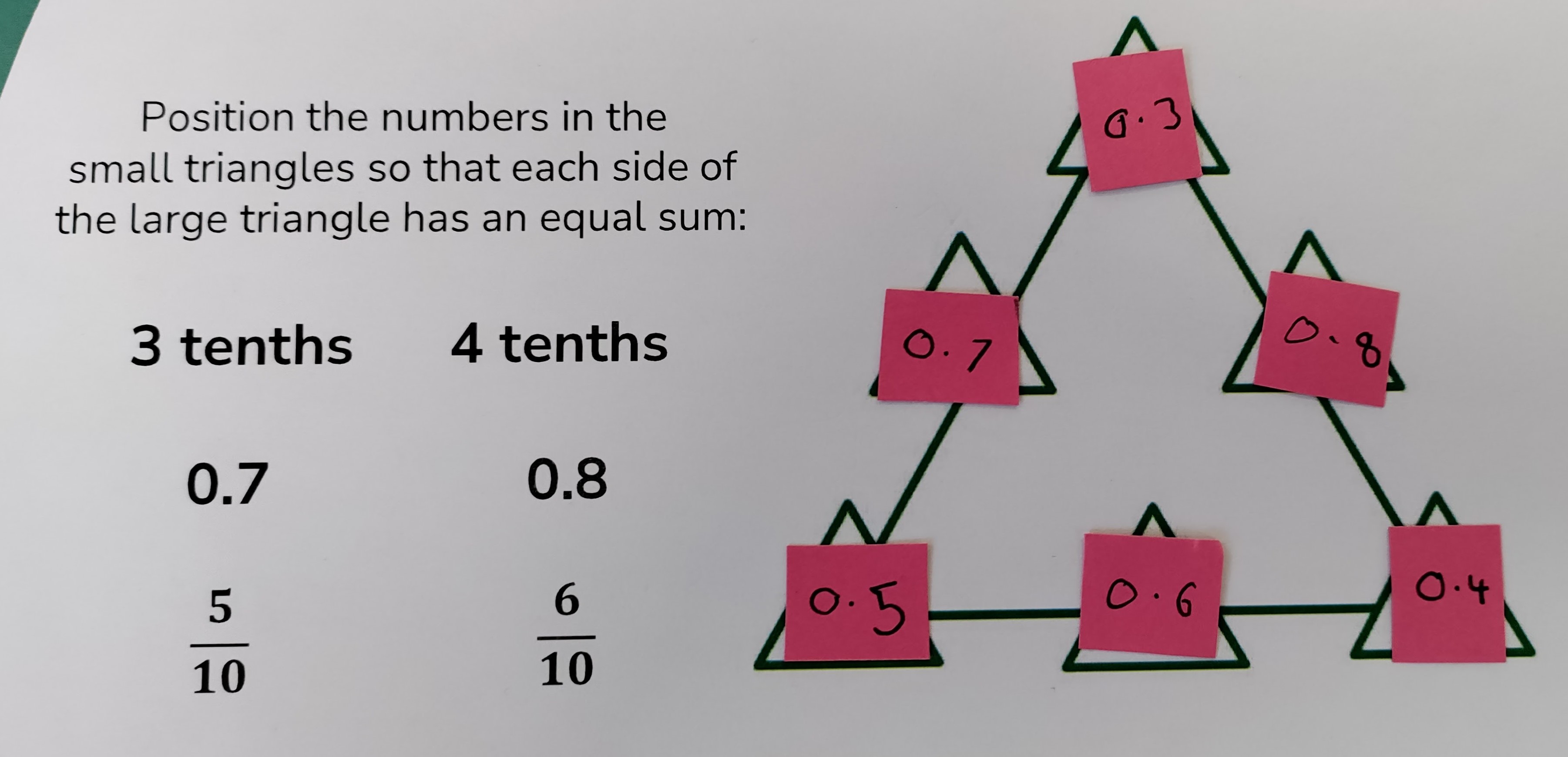
Children might see that each side of the large triangle has 3 little triangles along it. They might notice that each part is a number of tenths and comment that some are written in words, some as decimals and some as fractions.
It is important at this point that children understand how to translate between them, e.g., that 3 tenths could also be written as 0.3 or 3/10.
Scaffold for discussion, reasoning and problem-solving
Following this initial discussion, children could work in teams to talk through possibilities and strategies to solve the problem. Place value counters (tenths / 0.1 counters) would be a handy manipulative for working out how to lay out the groups so that they meet the parameters in the question.
Sentence frames could include:
I have noticed…
If… then…
I have noticed that the numbers are consecutive. They go up in tenths from 0.3 to 0.8.
If we use 0.8, 0.7 and 0.6 along one side then we won’t have enough tenths to make the other sides equal.
If confident with the addition and number facts required, sticky notes could support a ‘try then improve’ approach.
Suggestions for additional scaffolding
| Heuristics | Manipulatives | Word bank |
Try then improve Make a model | Place value counters | Total Sum Equal Parts Whole Difference |
Articulating strategies and sharing solutions
It is worth considering how children will share their problem-solving approaches and solutions.
Options could include:
- A classroom walk-around to view the solutions of other groups. One member of the group could remain at their table to share strategies with ‘visiting’ children.
- Listing 3 key points from their exploration for a spokesperson to share with the class
- Pairing up groups to share their strategies and solutions with each other
- Producing a team poster to show the process and final outcomes
- Writing a set of ‘how to’ instructions for how to solve a similar problem in the future
Evaluating strategies and considering metacognition
In maths, students develop or embed mathematical reasoning through talk, for example by articulating a mathematical proof or evaluating alternative methods.
‘We need to talk’, Oracy Education Commission, October 2024
As exemplified through case studies in the OEC report, focusing on process and efficiency, rather than simply getting the right answer, can develop children’s mathematical confidence, allowing them to talk their ideas through and build understanding of key concepts.
Reflection points to consider:
- When did things get challenging?
- What helped if you got stuck?
- What did you notice that helped you to decide on a strategy?
- Did your group try more than one strategy? Which one worked best in this case and why?
- How did your feelings change during the task?
- Did you have an ‘a-ha’ moment? When was it?
- What might you do differently next time?
The HFL Education Annual Maths Challenges are taking place in spring and summer 2025, with:
Challenges are hosted online for the heats and the final so your teams of four children can join in from the comfort of their own school.



